“五·一”期间,九年一班同学从学校出发,去距学校6千米的公园游玩,同学们分为步行和骑自行车两组,在去公园的全过程中,骑自行车的同学比步行的同学少用40分钟,已知骑自行车的速度是步行速度的3倍.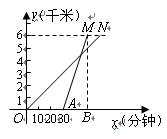
(1)求步行同学每小时走多少千米?
(2)图是两组同学前往公园时的路程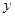 (千米)与时间
(千米)与时间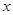 (分钟)的函数图象.
(分钟)的函数图象.
完成下列填空:
①表示骑车同学的函数图象是线段 ;
②已知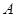 点坐标
点坐标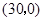 ,则
,则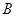 点的坐标为( ).
点的坐标为( ).
相关知识点
推荐套卷
“五·一”期间,九年一班同学从学校出发,去距学校6千米的公园游玩,同学们分为步行和骑自行车两组,在去公园的全过程中,骑自行车的同学比步行的同学少用40分钟,已知骑自行车的速度是步行速度的3倍.
(1)求步行同学每小时走多少千米?
(2)图是两组同学前往公园时的路程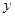 (千米)与时间
(千米)与时间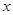 (分钟)的函数图象.
(分钟)的函数图象.
完成下列填空:
①表示骑车同学的函数图象是线段 ;
②已知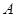 点坐标
点坐标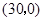 ,则
,则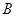 点的坐标为( ).
点的坐标为( ).