(本小题共14分)已知 是由满足下述条件的函数构成的集合:对任意
是由满足下述条件的函数构成的集合:对任意 ,①方程
,①方程 有实数根;②函数
有实数根;②函数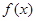 的导数
的导数 满足
满足 .
.
(Ⅰ)判断函数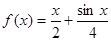 是否是集合
是否是集合 中的元素,并说明理由;
中的元素,并说明理由;
(Ⅱ)集合 中的元素
中的元素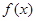 具有下面的性质:若
具有下面的性质:若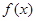 的定义域为
的定义域为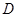 ,则对于任意
,则对于任意 ,都存在
,都存在 ,使得等式
,使得等式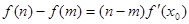 成立.试用这一性质证明:方程
成立.试用这一性质证明:方程 有且只有一个实数根;
有且只有一个实数根;
推荐套卷
(本小题共14分)已知 是由满足下述条件的函数构成的集合:对任意
是由满足下述条件的函数构成的集合:对任意 ,①方程
,①方程 有实数根;②函数
有实数根;②函数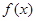 的导数
的导数 满足
满足 .
.
(Ⅰ)判断函数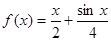 是否是集合
是否是集合 中的元素,并说明理由;
中的元素,并说明理由;
(Ⅱ)集合 中的元素
中的元素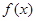 具有下面的性质:若
具有下面的性质:若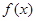 的定义域为
的定义域为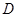 ,则对于任意
,则对于任意 ,都存在
,都存在 ,使得等式
,使得等式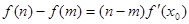 成立.试用这一性质证明:方程
成立.试用这一性质证明:方程 有且只有一个实数根;
有且只有一个实数根;