[北京]2012届北京市东城区高三上学期期末考试文科数学试卷
下列命题中正确的是
| A.如果两条直线都平行于同一个平面,那么这两条直线互相平行 |
| B.过一条直线有且只有一个平面与已知平面垂直 |
| C.如果一条直线平行于一个平面内的一条直线,那么这条直线平行于这个平面 |
| D.如果两条直线都垂直于同一平面,那么这两条直线共面 |
来源:2012届北京市东城区高三上学期期末考试文科数学试卷
函数 的图象如图所示,为了得到
的图象如图所示,为了得到 的图象,则只要将
的图象,则只要将 的图象
的图象 
A.向右平移 个单位长度 个单位长度 |
B.向右平移 个单位长度 个单位长度 |
C.向左平移 个单位长度 个单位长度 |
D.向左平移 个单位长度 个单位长度 |
来源:2012届北京市东城区高三上学期期末考试文科数学试卷
对于函数 ,有如下三个命题:
,有如下三个命题:
① 是偶函数;
是偶函数;
② 在区间
在区间 上是减函数,在区间
上是减函数,在区间 上是增函数;
上是增函数;
③ 在区间
在区间 上是增函数.
上是增函数.
其中正确命题的序号是 .(将你认为正确的命题序号都填上)
来源:2012届北京市东城区高三上学期期末考试文科数学试卷
在平面内,已知直线 ,点
,点 是
是 之间的定点,点
之间的定点,点 到
到 的距离分别为
的距离分别为 和
和 ,点
,点 是
是 上的一个动点,若
上的一个动点,若 ,且
,且 与
与 交于点
交于点 ,则
,则 面积的最小值为____.
面积的最小值为____.
来源:2012届北京市东城区高三上学期期末考试文科数学试卷
(本小题共13分)在等差数列 中,
中, ,其前
,其前 项和为
项和为 ,等比数列
,等比数列 的各项均为正数,
的各项均为正数, ,公比为
,公比为 ,且
,且 ,
,  .
.
(Ⅰ)求 与
与 ;
;
(Ⅱ)数列 满足
满足 ,求
,求 的前
的前 项和
项和 .
.
来源:2012届北京市东城区高三上学期期末考试文科数学试卷
(本小题共14分)如图,在四棱锥 中,底面
中,底面 是正方形,
是正方形, 平面
平面 ,
,  是
是 中点,
中点, 为线段
为线段 上一点.
上一点.
(Ⅰ)求证: ;
;
(Ⅱ)试确定点 在线段
在线段 上的位置,使
上的位置,使 //平面
//平面 ,并说明理由.
,并说明理由.
来源:2012届北京市东城区高三上学期期末考试文科数学试卷
(本小题共13分)已知函数
 .
.
(Ⅰ)若 ,求曲线
,求曲线 在点
在点 处的切线方程;
处的切线方程;
(Ⅱ)若函数 在区间
在区间 上单调递增,求实数
上单调递增,求实数 的取值范围.
的取值范围.
来源:2012届北京市东城区高三上学期期末考试文科数学试卷
(本小题共13分)已知椭圆 的右焦点为
的右焦点为 ,
, 为椭圆的上顶点,
为椭圆的上顶点, 为坐标原点,且△
为坐标原点,且△ 是等腰直角三角形.
是等腰直角三角形.
(Ⅰ)求椭圆的方程;
(Ⅱ)过点 分别作直线
分别作直线 ,
, 交椭圆于
交椭圆于 ,
, 两点,设两直线的斜率分别为
两点,设两直线的斜率分别为 ,
, ,且
,且 ,证明:直线
,证明:直线 过定点(
过定点( ).
).
来源:2012届北京市东城区高三上学期期末考试文科数学试卷
 ,
, ,则
,则



 在复平面上对应的点的坐标是
在复平面上对应的点的坐标是




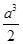
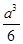

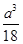
 ,且
,且 ,则
,则 



 :
: 上所有的点均在第二象限内,则实数
上所有的点均在第二象限内,则实数 的取值范围为
的取值范围为



 中,已知向量
中,已知向量 与
与 关于
关于 轴对称,向量
轴对称,向量 ,则满足不等式
,则满足不等式 的点
的点 的集合用阴影表示为
的集合用阴影表示为
 ,
,  ,若
,若 ,则
,则 的值为 .
的值为 . ,那么
,那么 的值为 .
的值为 . 那么
那么 的值为 .
的值为 . 中,若
中,若 ,则数列
,则数列 项和
项和 的最大值为 .
的最大值为 . 中,角
中,角 ,
, ,
, 的对边分别为
的对边分别为 ,
, ,
, ,且
,且 ,
, .
. ,求
,求 ;
;  ,求
,求 是由满足下述条件的函数构成的集合:对任意
是由满足下述条件的函数构成的集合:对任意 ,①方程
,①方程 有实数根;②函数
有实数根;②函数 的导数
的导数 满足
满足 .
. 是否是集合
是否是集合 ,则对于任意
,则对于任意 ,都存在
,都存在 ,使得等式
,使得等式 成立.试用这一性质证明:方程
成立.试用这一性质证明:方程 粤公网安备 44130202000953号
粤公网安备 44130202000953号