辽宁省高二下学期期末考试数学理科
若命题p(n)对n=k成立,则它对n=k+2也成立,又已知命题p(1)成立,则下列结论正确的是 ( )
| A.p(n)对所有自然数n都成立 | B.p(n)对所有正偶数n成立 |
| C.p(n)对所有正奇数n都成立 | D.p(n)对所有大于1的自然数n成立 |
已知甲、乙两车由同一起点同时出发,并沿同一路线(假定为直 线)行驶.甲车、
乙车的速度曲线分别为 (如右图所示).那么对于图中给定的
(如右图所示).那么对于图中给定的 ,下列判断中一
,下列判断中一
定正确的是( )
A.在 时刻,甲车在乙车前面 时刻,甲车在乙车前面 |
B. 时刻后,甲车在乙车后面 时刻后,甲车在乙车后面 |
C.在 时刻,两车的位置相同 时刻,两车的位置相同 |
D. 时刻后,乙车在甲车前面 时刻后,乙车在甲车前面 |
设θ是三角形的一个内角,且sinθ+cosθ=,则方程+=1所表示的曲线
为( )
| A.焦点在x轴上的椭圆 | B.焦点在y轴上的椭圆 |
C.焦点在x轴上 的双曲线 的双曲线 |
D.焦点在y轴上的双曲线 |
.如图所示,从双曲线-=1(a>0,b>0)的左焦点F引圆x2+y2=a2的切线,切
点为T,延长FT交双曲线右支于P点,若M为线段FP的中点,O为坐标原点,则|MO|-
|MT|与b-a的大小关系为 ( )
| A.|MO|-|MT|>b-a | B.|MO|-|MT|=b-a |
| C.|MO|-|MT|<b-a | D.不确定 |
已知点 、
、 ,
, 是直线
是直线 上任意一点,以
上任意一点,以 、
、 为
为
焦点的椭圆过点 .记椭圆离心率
.记椭圆离心率 关于
关于 的函数为
的函数为 ,那么下列结论正确的是( )
,那么下列结论正确的是( )
A. 与 与 一一对应 一一对应 |
B.函数 无最小值,有最大值 无最小值,有最大值 |
C.函数 是增函数 是增函数 |
D.函数 有最小值,无最大值 有最小值,无最大值 |
若椭圆 :
: (
( )和椭圆
)和椭圆 :
: 
( )的焦点相同且
)的焦点相同且 .给出如下四个结论:
.给出如下四个结论:
①椭圆 和椭圆
和椭圆 一定没有公共点; ②
一定没有公共点; ② ;
;
③ ; ④
; ④ .
.
其中,所有正确结论的序号是( )
| A.②③④ | B.①③④ | C.①②④ | D.①②③ |
设 ,
, 为不同的两点,直线
为不同的两点,直线 ,
, ,
,
以下命题中正确的序号为( ). 不论
不论 为何值,点N都不在直线
为何值,点N都不在直线 上;
上; 若
若 ,则过M,N的直线与直线
,则过M,N的直线与直线 平行;
平行; 若
若 ,则直线
,则直线 经过MN的中点;
经过MN的中点; 若
若 ,则点M、N在直线
,则点M、N在直线 的同侧且直线
的同侧且直线 与线段MN的延长线相交.
与线段MN的延长线相交.
| A.(1)(2)(3) | B.(2)(3)(4) | C.(1)(3)(4) | D.(1)(2)(3)(4) |
设 为区间
为区间 上的连续函数,且恒有
上的连续函数,且恒有 ,可以用随机模拟
,可以用随机模拟
方法近似计算积分 ,先产生两组(每组
,先产生两组(每组 个)区间
个)区间 上的均匀随机数
上的均匀随机数 和
和 ,由此得到
,由此得到 个点
个点 。再数出其中满足
。再数出其中满足 的点数
的点数 ,那么由随机模拟方法计算积分
,那么由随机模拟方法计算积分 的近似值为__
的近似值为__
五位同学围成一圈依序循环报数,规定:①第一位同学首次报出的数为1,第二位同学首次报出的数也为1,之后每位同学所报出的数都是前两位同学所报出的数之和;
②若报出的数为3的倍数,则报该数的同学需拍手一次.
已知甲同学第一个报数,当五位同学依序循环报到第100个数时,甲同学拍手的总次数为________.
(本小题满分12分)(1)对于定义在 上的函数
上的函数 ,满足
,满足 ,求证:函数
,求证:函数 在
在 上是减函数;
上是减函数;
(2)请你认真研读(1)中命题并联系以下命题:若 是定义在
是定义在 上的可导函数,满足
上的可导函数,满足 ,则
,则 是
是 上的减函数。然后填空建立一个普遍化的命题
上的减函数。然后填空建立一个普遍化的命题 :
:
设 是定义在
是定义在 上的可导函数,
上的可导函数, ,若
,若  +
+
 ,
,
则 是 上的减函数。
上的减函数。
注:命题的普遍化就是从考虑一个对象过渡到考虑包含该对象的一个集合;或者从考虑一个较小的集合过渡到考虑包含该较小集合的更大集合。
(3)证明(2)中建立的普遍化命题。
(本小题满分12分)已知函数 ,其图像记为
,其图像记为 ,若对于任意非零实数
,若对于任意非零实数 ,曲线
,曲线 与其在点
与其在点 处的切线交于另一点
处的切线交于另一点 ,曲线
,曲线 与其在点
与其在点 处的切线交于另一点
处的切线交于另一点 ,线段
,线段 ,
, 与曲线
与曲线 所围成封闭图形的面积分别记为
所围成封闭图形的面积分别记为 ,求证:
,求证: 为定值;
为定值;
(本小题满分12分)自然状态下的鱼类是一种可再生的资源,为了持续利用这一资源,需从宏观上考察其再生能力及捕捞强度对鱼群总量的影响。用 表示某鱼群在第
表示某鱼群在第 年初的总量,
年初的总量, ,且
,且 。不考虑其他因素,设在第
。不考虑其他因素,设在第 年内鱼群的繁殖量及被捕捞量都与
年内鱼群的繁殖量及被捕捞量都与 成正比,死亡量与
成正比,死亡量与 成正比,这些比例系数依次为正数
成正比,这些比例系数依次为正数 其中
其中 称为捕捞强度。
称为捕捞强度。
(1)求 与
与 的关系式;
的关系式;
(2)设 ,为了保证对任
,为了保证对任 意
意 ,都有
,都有 ,则捕捞强度
,则捕捞强度 的最大允许值是多少?证明你的结论。
的最大允许值是多少?证明你的结论。
(本小题满分12分)已知点 ,过点
,过点 作抛物线
作抛物线
 的切线
的切线 ,切点
,切点 在第二象限,如图.
在第二象限,如图.
(Ⅰ)求切点 的纵坐标;
的纵坐标;
(Ⅱ)若离心率为 的椭圆
的椭圆 恰好经过切点
恰好经过切点 ,设切线
,设切线 交椭圆的另一点为
交椭圆的另一点为 ,记切线
,记切线 的斜率分别为
的斜率分别为 ,若
,若 ,求椭圆方程.
,求椭圆方程.
选做题(本小题满分10分,请考生在第22、23、24三题中任选一题作答。如果多做,则按所做的第一题计分,作答时请在答题纸上所选题目的方框内打“√”。
22.选修4-1:几何证明选讲。
如图, 是圆
是圆 的直径,
的直径, 是弦,
是弦, 的平分线
的平分线 交圆
交圆 于点
于点 ,
, ,交
,交 的延长线于点
的延长线于点 ,
, 交
交 于点
于点 。
。
(1)求证: 是圆
是圆 的切线;
的切线;
(2)若 ,求
,求 的值。
的值。
选修4—4:坐标系与参数方程
在平面直角坐标系中,直线 过点
过点 且倾斜角为
且倾斜角为 ,以坐标原点为极点,
,以坐标原点为极点, 轴的非负半轴为极轴,建立极坐标系,曲线
轴的非负半轴为极轴,建立极坐标系,曲线 的极坐标方程为
的极坐标方程为 ,直线
,直线 与曲线
与曲线 相交于
相交于 两点;
两点;
(1)若 ,求直线
,求直线 的倾斜角
的倾斜角 的取值范围;
的取值范围;
(2)求弦 最短时直线
最短时直线 的参数方程。
的参数方程。
 对于
对于 的正整数
的正整数 均成立”时,第一步证明中的起始值
均成立”时,第一步证明中的起始值 应取( )
应取( )
 的值
的值 的部分图象,则函数
的部分图象,则函数 的零点所
的零点所




 在[1,2]内恒为正值的充要条件为( )
在[1,2]内恒为正值的充要条件为( )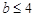



 复数
复数 在复平面上的对应点
在复平面上的对应点 的轨迹是
的轨迹是  答轨
答轨 迹类型不给分)
迹类型不给分)
 时水面上升的速度为
时水面上升的速度为 
 .
. 的单调性;
的单调性; 时,
时, 恒成立,求实数
恒成立,求实数 的取值范围;
的取值范围;
 .
.
 的值域;
的值域; ,若对
,若对 ,恒有
,恒有 成立,试求实数a的取值范围。
成立,试求实数a的取值范围。 粤公网安备 44130202000953号
粤公网安备 44130202000953号