(本小题满分12分)自然状态下的鱼类是一种可再生的资源,为了持续利用这一资源,需从宏观上考察其再生能力及捕捞强度对鱼群总量的影响。用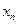 表示某鱼群在第
表示某鱼群在第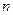 年初的总量,
年初的总量,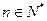 ,且
,且 。不考虑其他因素,设在第
。不考虑其他因素,设在第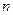 年内鱼群的繁殖量及被捕捞量都与
年内鱼群的繁殖量及被捕捞量都与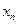 成正比,死亡量与
成正比,死亡量与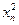 成正比,这些比例系数依次为正数
成正比,这些比例系数依次为正数 其中
其中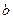 称为捕捞强度。
称为捕捞强度。
(1)求 与
与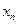 的关系式;
的关系式;
(2)设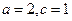 ,为了保证对任
,为了保证对任 意
意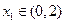 ,都有
,都有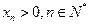 ,则捕捞强度
,则捕捞强度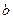 的最大允许值是多少?证明你的结论。
的最大允许值是多少?证明你的结论。
相关知识点
推荐套卷
(本小题满分12分)自然状态下的鱼类是一种可再生的资源,为了持续利用这一资源,需从宏观上考察其再生能力及捕捞强度对鱼群总量的影响。用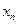 表示某鱼群在第
表示某鱼群在第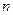 年初的总量,
年初的总量,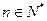 ,且
,且 。不考虑其他因素,设在第
。不考虑其他因素,设在第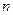 年内鱼群的繁殖量及被捕捞量都与
年内鱼群的繁殖量及被捕捞量都与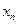 成正比,死亡量与
成正比,死亡量与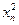 成正比,这些比例系数依次为正数
成正比,这些比例系数依次为正数 其中
其中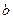 称为捕捞强度。
称为捕捞强度。
(1)求 与
与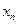 的关系式;
的关系式;
(2)设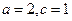 ,为了保证对任
,为了保证对任 意
意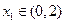 ,都有
,都有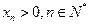 ,则捕捞强度
,则捕捞强度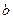 的最大允许值是多少?证明你的结论。
的最大允许值是多少?证明你的结论。