(本小题满分12分)(1)对于定义在 上的函数
上的函数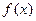 ,满足
,满足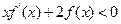 ,求证:函数
,求证:函数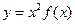 在
在 上是减函数;
上是减函数;
(2)请你认真研读(1)中命题并联系以下命题:若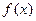 是定义在
是定义在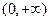 上的可导函数,满足
上的可导函数,满足 ,则
,则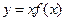 是
是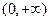 上的减函数。然后填空建立一个普遍化的命题
上的减函数。然后填空建立一个普遍化的命题 :
:
设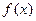 是定义在
是定义在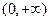 上的可导函数,
上的可导函数, ,若
,若  +
+
 ,
,
则 是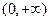 上的减函数。
上的减函数。
注:命题的普遍化就是从考虑一个对象过渡到考虑包含该对象的一个集合;或者从考虑一个较小的集合过渡到考虑包含该较小集合的更大集合。
(3)证明(2)中建立的普遍化命题。
相关知识点
推荐套卷
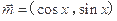 ,
, ,
,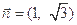 .
. ,求
,求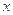 的值;
的值;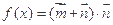 ,求函数
,求函数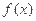 的值域.
的值域.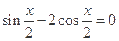 ,
,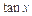 ;
;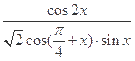 .
.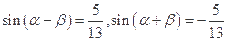 ,且
,且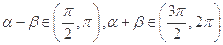 ,求
,求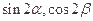 值.
值.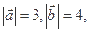 且
且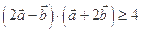 ,求
,求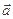 与
与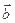 的夹角
的夹角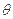 的取值范围.
的取值范围. )第一题满分5分,第二题满分5分,第三题满分8分.
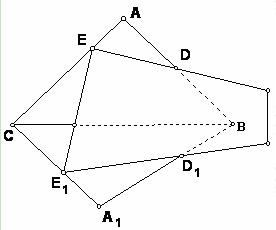
)第一题满分5分,第二题满分5分,第三题满分8分. 条交线ED,CB, E1 D1的关系。
条交线ED,CB, E1 D1的关系。 的值;
的值;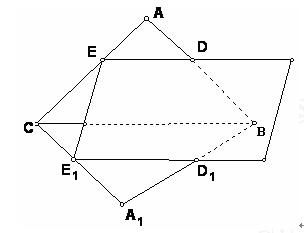
 粤公网安备 44130202000953号
粤公网安备 44130202000953号