(本小题满分12分)已知点 ,过点
,过点 作抛物线
作抛物线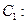
 的切线
的切线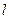 ,切点
,切点 在第二象限,如图.
在第二象限,如图.
(Ⅰ)求切点 的纵坐标;
的纵坐标;
(Ⅱ)若离心率为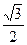 的椭圆
的椭圆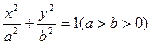 恰好经过切点
恰好经过切点 ,设切线
,设切线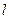 交椭圆的另一点为
交椭圆的另一点为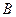 ,记切线
,记切线 的斜率分别为
的斜率分别为 ,若
,若 ,求椭圆方程.
,求椭圆方程.
推荐套卷
(本小题满分12分)已知点 ,过点
,过点 作抛物线
作抛物线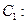
 的切线
的切线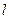 ,切点
,切点 在第二象限,如图.
在第二象限,如图.
(Ⅰ)求切点 的纵坐标;
的纵坐标;
(Ⅱ)若离心率为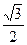 的椭圆
的椭圆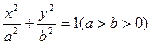 恰好经过切点
恰好经过切点 ,设切线
,设切线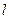 交椭圆的另一点为
交椭圆的另一点为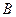 ,记切线
,记切线 的斜率分别为
的斜率分别为 ,若
,若 ,求椭圆方程.
,求椭圆方程.