高考数学总复习考点引领+技巧点拨第八章第5课时练习卷
若等腰直角三角形的直角边长为2,则以一直角边所在的直线为轴旋转一周所成的几何体体积是__________.
已知圆锥的侧面展开图是一个半径为3cm,圆心角为 的扇形,则此圆锥的高为________cm.
的扇形,则此圆锥的高为________cm.
已知正方形ABCD的边长为2,E、F分别为BC、DC的中点,沿AE、EF、AF折成一个四面体,使B、C、D三点重合,则这个四面体的体积为________.
如图所示,正方体ABCDA1B1C1D1的棱长为6,则以正方体ABCDA1B1C1D1的中心为顶点,以平面AB1D1截正方体外接球所得的圆为底面的圆锥的全面积为________.
如图,在球面上有四个点P、A、B、C,如果PA、PB、PC两两互相垂直,且PA=PB=PC=a,求这个球的表面积.
如图①所示,在Rt△ABC中,AC=6,BC=3,∠ABC=90°,CD为∠ACB的平分线,点E在线段AC上,CE=4.如图②所示,将△BCD沿CD折起,使得平面BCD⊥平面ACD,连结AB,设点F是AB的中点. 图①
图① 图②
图②
(1)求证:DE⊥平面BCD;
(2)若EF∥平面BDG,其中G为直线AC与平面BDG的交点,求三棱锥B-DEG的体积.
在△ABC中,∠BAC=90°,∠B=60°,AB=1,D为线段BC的中点,E、F为线段AC的三等分点(如图①).将△ABD沿着AD折起到△AB′D的位置,连结B′C(如图②).
图①
图②
(1)若平面AB′D⊥平面ADC,求三棱锥B′-ADC的体积;
(2)记线段B′C的中点为H,平面B′ED与平面HFD的交线为l,求证:HF∥l;
(3)求证:AD⊥B′E.
在边长为a的正三角形铁皮的三个角切去三个全等的四边形,再把它的边沿虚线折起(如图),做成一个无盖的正三角形底铁皮箱,当箱底边长为多少时,箱子容积最大?最大容积是多少?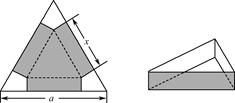
四面体的六条棱中,有五条棱长都等于a.
(1)求该四面体的体积的最大值;
(2)当四面体的体积最大时,求其表面积.
如图,底面边长为a,高为h的正三棱柱ABC-A1B1C1,其中D是AB的中点,E是BC的三等分点.求几何体BDEA1B1C1的体积.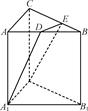
如图,已知正三棱柱ABCA1B1C1的底面边长为2cm,高为5cm,则一质点自点A出发,沿着三棱柱的侧面绕行两周到达点A1的最短路线的长为________cm.
一个圆锥的侧面展开图是圆心角为 π,半径为18cm的扇形,则圆锥母线与底面所成角的余弦值为________.
π,半径为18cm的扇形,则圆锥母线与底面所成角的余弦值为________.
如图所示,在正三棱锥S-ABC中,M、N分别是SC、BC的中点,且MN⊥AM,若侧棱SA=2 ,则正三棱锥SABC外接球的表面积是________.
,则正三棱锥SABC外接球的表面积是________.
我国古代数学名著《数书九章》中有“天池盆测雨”题:在下雨时,用一个圆台形的天池盆接雨水.天池盆盆口直径为二尺八寸,盆底直径为一尺二寸,盆深一尺八寸.若盆中积水深九寸,则平地降雨量是________寸.(注:①平地降雨量等于盆中积水体积除以盆口面积;②一尺等于十寸)
如图,四棱锥P-ABCD中,PA⊥底面ABCD,AB⊥AD,点E在线段AD上,且CE∥AB.
(1)求证:CE⊥平面PAD;
(2)若PA=AB=1,AD=3,CD= ,∠CDA=45°,求四棱锥P-ABCD的体积.
,∠CDA=45°,求四棱锥P-ABCD的体积.
如图所示,已知三棱柱ABC-A1B1C1的所有棱长均为1,且AA1⊥底面ABC,则三棱锥B1-ABC1的体积为________.
一个球与一个正三棱柱的三个侧面和两个底面都相切,已知这个球的体积是 π,那么这个三棱柱的体积是________.
π,那么这个三棱柱的体积是________.
如图,在四边形ABCD中,∠DAB=90°,∠ADC=135°,AB=5,CD=2 ,AD=2,求四边形ABCD绕AD旋转一周所成几何体的表面积及体积.
,AD=2,求四边形ABCD绕AD旋转一周所成几何体的表面积及体积.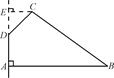
 ,
, ,
, ,则此长方体的外接球的表面积是________.
,则此长方体的外接球的表面积是________.
 粤公网安备 44130202000953号
粤公网安备 44130202000953号