如图①所示，在Rt△ABC中，AC＝6，BC＝3，∠ABC＝90°，CD为∠ACB的平分线，点E在线段AC上，CE＝4.如图②所示，将△BCD沿CD折起，使得平面BCD⊥平面ACD，连结AB，设点F是AB的中点．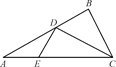
图①
图②
(1)求证：DE⊥平面BCD；
(2)若EF∥平面BDG，其中G为直线AC与平面BDG的交点，求三棱锥B-DEG的体积．
相关试题
的焦点为
，抛物线
的焦点为
．
与抛物线
有且只有一个交点，求直线
与抛物线
．
两点，求
的面积．
中，已知角
．
．
的对边分别为
，且
．
，试判断
的前
项和为
，
，
．
的前
，求证：
．如图，在平面直角坐标系
中，椭圆
过点
，离心率
，
为椭圆的左右焦点．
（1）求椭圆
的标准方程；
（2）设圆
的圆心
在
轴上方，且圆经过椭圆两焦点．点
为椭圆上的一动点，
与圆相切于点
．
①当
时，求直线的方程；
②当取得最大值为
时，求圆方程．
的棱长为
，
为棱
上的一动点．
的体积
面
面相关知识点
推荐套卷
粤公网安备 44130202000953号