椭圆C：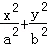
=1（a＞b＞0）的两个焦点分别为F1（﹣c，0），F2（c，0），M是椭圆短轴的一个端点，且满足
=0，点N（ 0，3 ）到椭圆上的点的最远距离为5
（1）求椭圆C的方程
（2）设斜率为k（k≠0）的直线l与椭圆C相交于不同的两点A、B，Q为AB的中点，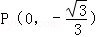
；问A、B两点能否关于过点P、Q的直线对称？若能，求出k的取值范围；若不能，请说明理由．
相关试题
的值；
的定义域为R，
．
的值；
在区间
上为增函数；
，证明函数
在
上有零点．
是边长为1的正方形，
，
，E是侧棱SC上的一点．
；
在区间[-2，0]上单调递减，若
，求实数
的取值范围
中，
．
推荐套卷
椭圆C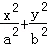：=1（a＞b＞0）的两个焦点分别为F1（﹣c，0），F2（c，0），M是椭圆短轴的一个端点，且满足=0，点N（ 0，3 ）到椭圆上的点的最远距离为5
（1）求椭圆C的方程
（2）设斜率为k（k≠0）的直线l与椭圆C相交于不同的两点A、B，Q为AB的中点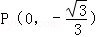，；问A、B两点能否关于过点P、Q的直线对称？若能，求出k的取值范围；若不能，请说明理由．
粤公网安备 44130202000953号