2013年全国统一高考文科数学试卷(上海卷)
某学校高一年级男生人数占该年级学生人数的40%,在一次考试中,男,女平均分数分别为75、80,则这次考试该年级学生平均分数为.
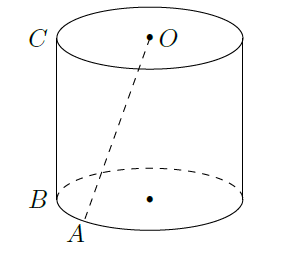
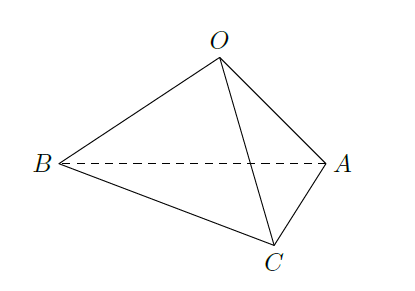
已知圆柱
的母线长为l,底面半径为
,
是上底面圆心,
是下底面圆周上两个不同的点,
是母线,如图,若直线
与
所成角的大小为
,则
=.
盒子中装有编号为1,2,3,4,5,6,7的七个球,从中任意抽取两个,则这两个球的编号之积为偶数的概率是(结果用最简分数表示).
已知正方形 的边长为1,记以 为起点,其余顶点为终点的向量分别为 ;以 为起点,其余顶点为终点的向量分别为 ,若 ,且 ,则 的最小值是.
钱大姐常说"好货不便宜",她这句话的意思是:"好货"是"不便宜"的()
| A. | 充分条件 | B. | 必要条件 |
| C. | 充分必要条件 | D. | 既非充分又非必要条件 |
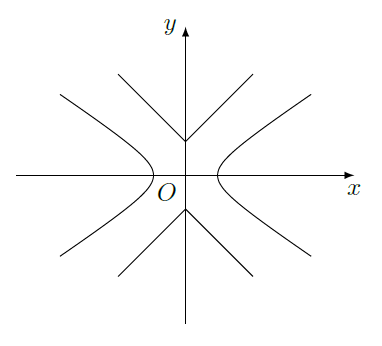
记椭圆 围成的区域(含边界)为Ω ( 1,2,…),当点 分别在Ω1,Ω2,…上时, 的最大值分别是 ,则 =( )
| A. | 0 | B. | C. | 2 | D. |
甲厂以
千克/小时的速度匀速生产某种产品(生产条件要求
),每一小时可获得的利润是
元.
(1)求证:生产
千克该产品所获得的利润为
元;
(2)要使生产900千克该产品获得的利润最大,问:甲厂应该选取何种生产速度?并求此最大利润.
已知函数
,其中常数
(1)令
,判断函数
的奇偶性,并说明理由;
(2)令
,将函数
的图象向左平移个
单位,再向上平移1个单位,得到函数
的图象,对任意
,求
在区间
上零点个数的所有可能值.
已知函数
,无穷数列
满足
,
.
(1)若
,求
;
(2)若
,且
成等比数列,求
的值
(3)是否存在
,使得
成等差数列?若存在,求出所有这样的
,若不存在,说明理由.
 粤公网安备 44130202000953号
粤公网安备 44130202000953号