2013年全国统一高考理科数学试卷(陕西卷)
根据下列算法语句, 当输入 为60时, 输出 的值为()

| A. | 25 | B. | 30 | C. | 31 | D. | 61 |
设 , 为向量, 则" "是" "的()
| A. | 充分不必要条件 | B. | 必要不充分条件 |
| C. | 充分必要条件 | D. | 既不充分也不必要条件 |
某单位有840名职工, 现采用系统抽样方法, 抽取42人做问卷调查, 将840人按1, 2, …, 840随机编号, 则抽取的42人中, 编号落入区间[481, 720]的人数为()
| A. | 11 | B. | 12 | C. | 13 | D. | 14 |
如图, 在矩形区域
的
,
两点处各有一个通信基站, 假设其信号覆盖范围分别是扇形区域
和扇形区域
(该矩形区域内无其他信号来源, 基站工作正常). 若在该矩形区域内随机地选一地点, 则该地点无信号的概率是 ( )
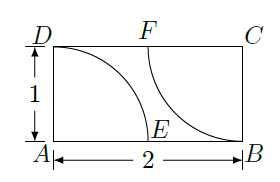
| A. | B. | C. | D. |
设 是复数, 则下列命题中的假命题是 ( )
| A. | 若 , 则 | B. | 若 , 则 |
| C. | 若 , 则 | D. | 若 , 则 |
设 的内角 所对的边分别为 , 若 , 则 的形状为()
| A. | 锐角三角形 | B. | 直角三角形 | C. | 钝角三角形 | D. | 不确定 |
设函数  , 则当 时, 表达式的展开式中常数项为()
| A. | -20 | B. | 20 | C. | -15 | D. | 15 |
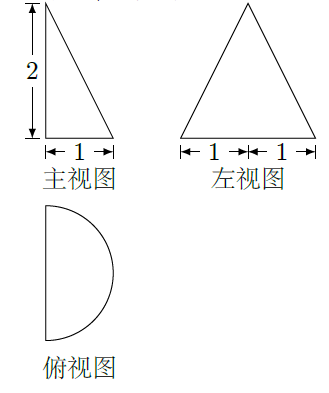
在如图所示的锐角三角形空地中, 欲建一个面积不小于300m2的内接矩形花园(阴影部分), 则其边长
(单位
)的取值范围是 ( )

| A. | [15,20] | B. | [12,25] | C. | [10,30] | D. | [20,30] |
如图, 四棱柱
的底面
是正方形,
为底面中心,
平面
,
.
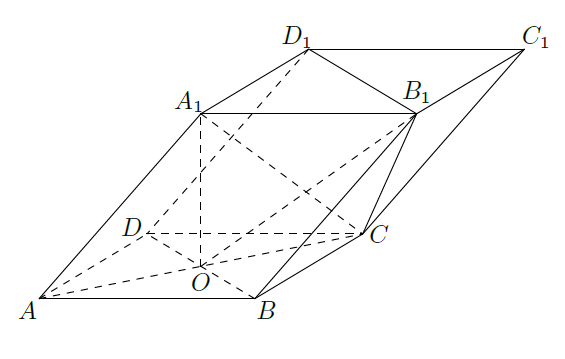
(Ⅰ) 证明:
平面
;
(Ⅱ) 求平面
与平面
的夹角
的大小.
在一场娱乐晚会上, 有5位民间歌手(1至5号)登台演唱, 由现场数百名观众投票选出最受欢迎歌手. 各位观众须彼此独立地在选票上选3名选手, 其中观众甲是1号歌手的歌迷, 他必选1号, 不选2号, 另在3至5号中随机选2名. 观众乙和丙对5位歌手的演唱没有偏爱, 因此在1至5号中随机选3名歌手.
(Ⅰ) 求观众甲选中3号歌手且观众乙未选中3号歌手的概率;
(Ⅱ)
表示3号歌手得到观众甲、乙、丙的票数之和, 求
的分布列和数学期望.
已知动圆过定点
, 且在
轴上截得的弦
的长为8.
(Ⅰ) 求动圆圆心的轨迹
的方程;
(Ⅱ) 已知点
, 设不垂直于
轴的直线
与轨迹
交于不同的两点
, 若
轴是
的角平分线, 证明直线
过定点.
 粤公网安备 44130202000953号
粤公网安备 44130202000953号