2013年全国统一高考文科数学试卷(全国Ⅱ卷)
设椭圆C: 的左、右焦点分别为 、 ,P是C上的点, ⊥ , ,则C的离心率为()
| A. | B. | C. | D. |
一个四面体的顶点在空间直角坐系 中的坐标分别是(1,0,1),(1,1,0),(0,1,1),(0,0,0),画该四面体三视图中的正视图时,以 平面为投影面,则得到的正视图可为()




设抛物线 的焦点为 ,直线 过 且与 交于 两点.若 ,则 的方程为()
| A. | 或 |
| B. | 或 |
| C. | 或 |
| D. | 或 |
已知函数 ,下列结论中错误的是()
| A. | |
| B. | 函数 的图像是中心对称图形 |
| C. | 若 是 的极小值点,则 在区间 单调递减 |
| D. | 若 是 的极值点,则 |
若存在正数 使 成立,则 的取值范围是( )
| A. | (-∞,+∞) | B. | (-2, +∞) | C. | (0, +∞) | D. | (-1,+∞) |
经销商经销某种农产品,在一个销售季度内,每售出1
该产品获利润500元,未售出的产品,每1
亏损300元.根据历史资料,得到销售季度内市场需求量的频率分布直图,如下图所示.经销商为下一个销售季度购进了130
该农产品.以 (单位:
,100≤
≤150)表示下一个销售季度内的市场需求量,
(单位:元)表示下一个销售季度内经销该农产品的利润.
(单位:
,100≤
≤150)表示下一个销售季度内的市场需求量,
(单位:元)表示下一个销售季度内经销该农产品的利润.
(Ⅰ)将
表示为
的函数;
(Ⅱ)根据直方图估计利润
不少于57000元的概率.
在平面直角坐标系
中,己知圆
在
上截得线段长为
,在
轴上截得线段长为
.
(Ⅰ)求圆心
的轨迹方程;
(Ⅱ)若
点到直线
的距离为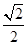 ,求圆
的方程.
,求圆
的方程.
己知函数
.
(I)求
的极小值和极大值;
(II)当曲线
的切线
的斜率为负数时,求
在
轴上截距的取值范围.
如图,
为
外接圆的切线,
的延长线交直线
于点
,
分别为弦
与弦
上的点,且
四点共圆.

证明:
(Ⅰ)
是
外接圆的直径;
(Ⅱ)若
.求过
四点的圆的面积与
外接圆面积的比值.
已知动点 , 都在曲线C: ( 为参数)上,对应参数分别为 与 ( ), 为 的中点。
(Ⅰ)求
的轨迹的参数方程
(Ⅱ)将
到坐标原点的距离
表示为
的函数,并判断
的轨迹是否过坐标原点。


 粤公网安备 44130202000953号
粤公网安备 44130202000953号