经销商经销某种农产品,在一个销售季度内,每售出1
该产品获利润500元,未售出的产品,每1
亏损300元.根据历史资料,得到销售季度内市场需求量的频率分布直图,如下图所示.经销商为下一个销售季度购进了130
该农产品.以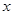 (单位:
,100≤
≤150)表示下一个销售季度内的市场需求量,
(单位:元)表示下一个销售季度内经销该农产品的利润.
(单位:
,100≤
≤150)表示下一个销售季度内的市场需求量,
(单位:元)表示下一个销售季度内经销该农产品的利润.
(Ⅰ)将
表示为
的函数;
(Ⅱ)根据直方图估计利润
不少于57000元的概率.
相关知识点
推荐套卷
 及对应的一个特征向量
及对应的一个特征向量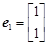 ,并且矩阵M对应的变换将点
,并且矩阵M对应的变换将点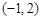 变换成
变换成 ,求矩阵M..
,求矩阵M..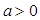 ,两个函数
,两个函数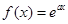 ,
,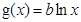 的图像关于直线
的图像关于直线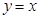 对称.
对称.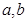 满足的关系式;
满足的关系式;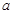 取何值时,函数
取何值时,函数 有且只有一个零点;
有且只有一个零点;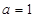 时,在
时,在 上解不等式
上解不等式 .
.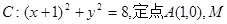 为圆上一动点,点
为圆上一动点,点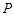 是线段
是线段 的垂直平分线与直线
的垂直平分线与直线 的交点.
的交点.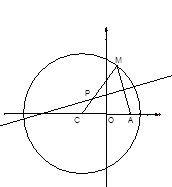
 的方程;
的方程; 是曲线
是曲线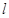 的方程;(不要求证明)
的方程;(不要求证明)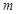 过切点
过切点 关于直线
关于直线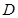 ,证明:直线
,证明:直线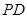 恒过一定点,并求定点的坐标.
恒过一定点,并求定点的坐标.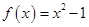 ,设曲线
,设曲线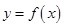 在点
在点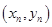 处的切线与
处的切线与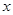 轴的交点为
轴的交点为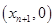 ,其中
,其中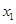 为正实数.
为正实数.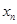 表示
表示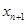 ;
;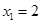 ,若
,若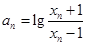 ,试证明数列
,试证明数列 为等比数列,并求数列
为等比数列,并求数列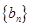 的前
的前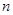 项和
项和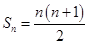 ,记数列
,记数列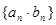 的前
的前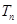 ,求
,求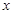 元.公司拟投入
元.公司拟投入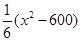 万元作为技改费用,投入50万元作为固定宣传费用,投入
万元作为技改费用,投入50万元作为固定宣传费用,投入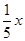 万元作为浮动宣传费用.试问:当该商品明年的销售量
万元作为浮动宣传费用.试问:当该商品明年的销售量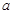 至少应达到多少万件时,才可能使明年的销售收入不低于原收入与总投入之和?并求出此时商品的每件定价.
至少应达到多少万件时,才可能使明年的销售收入不低于原收入与总投入之和?并求出此时商品的每件定价. 粤公网安备 44130202000953号
粤公网安备 44130202000953号