全国重点高中提前招生真题过关(十)
如图所示,有一电路连着三个开关,每个开关闭合与断开是等可能的,若不考虑元件的故障因素,则电灯点亮的概率为( )

| A. |
|
B. |
|
C. |
|
D. |
|
如图,在圆心角为直角的扇形 中,分别以 为直径作两个半圆向直角扇形 内随机取一点,则该点刚好来自阴影部分的概率是( )
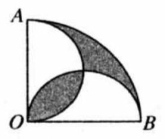
| A. |
|
B. |
|
C. |
|
D. |
|
有 张形状、大小、质地均相同的卡片,正面分别印有数字 ,背面完全相同.现将这 张卡片洗匀后正面向下放在桌子上,从中随机抽取一张,抽出的卡片正面印有的数字恰好是奇数的概率为( )
| A. |
|
B. |
|
C. |
|
D. |
|
如图,一小球从三角仪器的入口处落下,当它依次碰到每层菱形挡块时,向左或向右落下的可能性相同.则小球通过第二层 位置和第三层 位置的概率分别是( )

| A. |
|
B. |
|
C. |
|
D. |
|
将一枚六个面编号分别为 的质地均匀的正方体骰子先后投掷两次,记第一次掷出的点数为 ,第二次掷出的点数为 ,则使关于 的方程组 只有正数解的概率为( )
| A. |
|
B. |
|
C. |
|
D. |
|
杭州市某公交站每天 开往某学校的三辆班车票价相同,但车的舒适程度不同.学生小杰先观察后上车,当第一辆车开来时,他不上车,而是仔细观察车的舒适状况,若第二辆车的状况比第一辆车好,他就上第二辆车;若第二辆车不如第一辆车,他就上第三辆车.若按这三辆车的舒适程度分为优、中、差三等,则小杰坐上优等车的概率是( )
| A. |
|
B. |
|
C. |
|
D. |
|
我们对一个三角形的顶点和边都赋给一个特征值,并定义:从任意顶点出发,沿顺时针或逆时针方向依次将顶点和边的特征值相乘,再把三个乘积相加,所得之和称为此三角形的顺序旋转和或逆序旋转和.如图① 是该三角形的顺序旋转和, 是该三角形的逆序旋转和.已知某三角形的特征值如图②,若从 中任取一个数作为 ,从 中任取一个数作为 ,则对任意正整数 ,此三角形的顺序旋转和与逆序旋转和的差都小于 的概率是_____.

如图,用红蓝黄三色将图中区域 染色,要求有公共边界的相邻区域不能染成相同的颜色.则满足区域 恰好染成蓝色的概率是_____.

为了参加全市中学生“党史知识竞赛”,某校准备从甲、乙 名女生和丙、丁 名男生中任选 人代表学校参加比赛.
(1)如果已经确定女生甲参加,再从其余的候选入中随机选取 人,则女生乙被选中的概率是_____.
(2)所选代表恰好为 名女生和 名男生的概率为_____.
2020年某校将迎来70周年校庆,学校安排 位男老师和 位女老师一起筹办大型文艺晩会,并随机地从中抽取 位老师主持晩会,则最后确定的主持人是一男一女的概率为_____.
从 这 个数中随机抽取一个数,记为 ,若数 使关于 的不等式组 无解,且使关于 的分式方程 有非负整数解,那么从这 个数中抽到满足条件的 的概率是_____.
一枚质地均匀的正方体骰子的六个面上的数字分别是 ;另一枚质地均匀的正方体骰子的六个面上的数字分别是 .同时掷这两枚骰子,则其朝上的面两数字之和为奇数 的概率是_____.
某广场地面铺满了边长为 的正六边形地砖.现在向上抛掷半径为 的圆碟,圆碟落地后与地砖间的间隙不相交的概率大约是_____.
2021年,黄冈、咸宁、孝感三市实行中考联合命题,为确保联合命题的公平性,决定采取三轮抽签的方式来确定各市选派命题组长的学科.第一轮,各市从语文、数学、英语三个学科中随机抽取一科;第二轮,各市从物理、化学、历史三个学科中随机抽取一科;第三轮,各市从道德与法治、地理、生物三个学科中随机抽取一科.
(1)黄冈在第一轮抽到语文学科的概率是_____.
(2)用画树状图或列表法求黄冈在第二轮和第三轮抽签中,抽到的学科恰好是历史和地理的概率.
甲、乙、丙三人之间相互传球,球从一个人手中随机传到另外一个人手中,共传球三次.
(1)若开始时球在甲手中,求经过三次传球后,球传回到甲手中的概率是多少?
(2)若乙想使球经过三次传递后,球落在自己手中的概率最大,乙会让球开始时在谁手中?请说明理由.
在一个不透明的布袋里装有 个标有 的小球,它们的形状、大小完全相同.小明从布袋里随机取出一个小球,记下数字为 ,小红在剩下的 个小球中随机取出一个小球,记下数字为 ,这样确定了点 的坐标 .
(1)画树状图或列表,写出点 所有可能的坐标;
(2)求点 在函数 的图象上的概率;
(3)小明和小红约定做一个游戏,其规则为:若 满足 则小明胜;若 满足 则小红胜,这个游戏公平吗?说明理由;若不公平,请写出公平的游戏规则.
假设有一个正八面体的骰子,八个面上分别写上了 这 个数字,每一次投掷这个骰子,出现这 个数字的机会都是一样的.若将骰子掷三次,依次记录朝上的面上三次出现的数字,设出现的数字中最大的一个用 表示,最小的一个用 表示.
(1)令 ,求 的取值范围;
(2)求 的概率.
口袋中有 个相同的小球,它们分别写有数字 ,从口袋中随机取出两个球,用所得的两个数 和 构成函数 和 ,求使这两个函数的交点在直线 右侧的概率.
 粤公网安备 44130202000953号
粤公网安备 44130202000953号