2020年全国统一高考理科数学试卷(新课标Ⅲ)
在一组样本数据中,1,2,3,4出现的频率分别为 ,且 ,则下面四种情形中,对应样本的标准差最大的一组是( )
| A. |
|
B. |
|
| C. |
|
D. |
|
Logistic模型是常用数学模型之一,可应用于流行病学领城.有学者根据公布数据建立了某地区新冠肺炎累计确诊病例数 I( t)( t的单位:天)的 Logistic模型: ,其中 K为最大确诊病例数.当 I( )=0.95 K时,标志着已初步遏制疫情,则 约为( )(ln19≈3)
| A. |
60 |
B. |
63 |
C. |
66 |
D. |
69 |
设 为坐标原点,直线 与抛物线 C: 交于 , 两点,若 ,则 的焦点坐标为( )
| A. |
|
B. |
|
C. |
|
D. |
|
下图为某几何体的三视图,则该几何体的表面积是( )
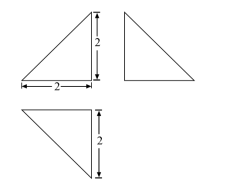
| A. |
6+4 |
B. |
4+4 |
C. |
6+2 |
D. |
4+2 |
已知2tan θ-tan( θ+ )=7,则tan θ=( )
| A. |
-2 |
B. |
-1 |
C. |
1 |
D. |
2 |
若直线 l与曲线 y= 和 x 2+ y 2= 都相切,则 l的方程为( )
| A. |
y=2x+1 |
B. |
y=2x+ |
C. |
y= x+1 |
D. |
y= x+ |
设双曲线 C: ( a>0, b>0)的左、右焦点分别为 F 1, F 2,离心率为 . P是 C上一点,且 F 1 P⊥ F 2 P.若△ PF 1 F 2的面积为4,则 a=( )
| A. |
1 |
B. |
2 |
C. |
4 |
D. |
8 |
已知5 5<8 4,13 4<8 5.设 a=log 53, b=log 85, c=log 138,则( )
| A. |
a<b<c |
B. |
b<a<c |
C. |
b<c<a |
D. |
c<a<b |
关于函数 f( x)= 有如下四个命题:
| A. |
①f(x)的图像关于y轴对称. |
| B. |
②f(x)的图像关于原点对称. |
| C. |
③f(x)的图像关于直线x= 对称. |
| D. |
④f(x)的最小值为2. |
其中所有真命题的序号是__________.
设数列{an}满足a1=3, .
(1)计算a2,a3,猜想{an}的通项公式并加以证明;
(2)求数列{2nan}的前n项和Sn.
某学生兴趣小组随机调查了某市100天中每天的空气质量等级和当天到某公园锻炼的人次,整理数据得到下表(单位:天):
锻炼人次 空气质量等级 |
[0,200] |
(200,400] |
(400,600] |
1(优) |
2 |
16 |
25 |
2(良) |
5 |
10 |
12 |
3(轻度污染) |
6 |
7 |
8 |
4(中度污染) |
7 |
2 |
0 |
(1)分别估计该市一天的空气质量等级为1,2,3,4的概率;
(2)求一天中到该公园锻炼的平均人次的估计值(同一组中的数据用该组区间的中点值为代表);
(3)若某天的空气质量等级为1或2,则称这天"空气质量好";若某天的空气质量等级为3或4,则称这天"空气质量不好".根据所给数据,完成下面的2×2列联表,并根据列联表,判断是否有95%的把握认为一天中到该公园锻炼的人次与该市当天的空气质量有关?
人次≤400 |
人次>400 |
|
空气质量好 |
||
空气质量不好 |
附: ,
P( K 2≥ k) |
0.050 |
0.010 |
0.001 |
k |
3.841 |
6.635 |
10.828 |
如图,在长方体 中,点 分别在棱 上,且 , .

(1)证明:点 在平面 内;
(2)若
,
,  ,求二面角
的正弦值.
,求二面角
的正弦值.
已知椭圆 的离心率为 , , 分别为 的左、右顶点.
(1)求 的方程;
(2)若点 在 上,点 在直线 上,且 , ,求 的面积.
设函数 ,曲线 在点( ,f( ))处的切线与y轴垂直.
(1)求b.
(2)若 有一个绝对值不大于1的零点,证明: 所有零点的绝对值都不大于1.
在直角坐标系xOy中,曲线C的参数方程为 (t为参数且t≠1),C与坐标轴交于A、B两点.
(1)求 ;
(2)以坐标原点为极点,x轴正半轴为极轴建立极坐标系,求直线AB的极坐标方程.
 粤公网安备 44130202000953号
粤公网安备 44130202000953号