2016年辽宁省鞍山市中考数学试卷
如图这是小刚玩投掷飞镖的游戏,他设计了一个如图所示的靶子,点 、 分别是矩形 的两边 、 上的点, ,点 、 是 上任意两点,则投掷一次,飞镖落在阴影部分的概率是

A. B. C. D.
如图,点 是矩形 的边 上的点, ,将矩形沿着过点 的直线翻折后,点 、 分别落在边 下方的点 、 处,且点 、 、 在同一条直线上,折痕与边 交于点 , 与 交于点 .若 ,那么 的周长为

A. B. C. D.6
如图,在 中, , , 于点 ,点 、 、 分别是边 、 、 的中点,连接 、 ,动点 从点 出发,以每秒2个单位长度的速度向点 方向运动,(点 运动到 的中点时停止);过点 作直线 与线段 交于点 ,以 为斜边作 ,点 在 上,设运动的时间为 与矩形 重叠部分的面积为 ,则 与 之间的函数关系图象大致为
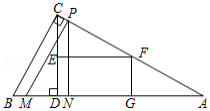
A. B.
B.
C. D.
D.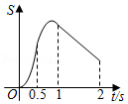
某工厂一月份生产收入100万元,第一季度共生产了 月份累计收入达到364万元,若2、3月份的生产收入平均增长率为 ,则可列方程为 .
某校举行学生会成员的竞选活动,对竞选者从平时表现、民主测评和演讲三个方面按百分制打分,然后以 的比例来计算最终成绩.若一名同学的平时表现、民主测评和演讲成绩分别为90分,80分,94分,则这名同学的最终成绩为 分.
如图,在平面直角坐标系中有直线 与双曲线 在直线上取点 ,过点 作 轴的垂线交双曲线于点 ,过 作 轴的垂线交直线于点 ,过点 作 轴的垂线交双曲线于点 ,过 作 轴的垂线交双曲线于点 过 作 轴的垂线交直线于点 , ,按此规律继续操作下去,依次得到直线上的点 , , , ,记点 的横坐标为 ,若 ,则 .

如图,在正方形 中,对角线 、 相交于点 , 的平分线 交 于点 ,交 于点 ,下列四个结论,其中正确的是 (填序号即可).
①
②
③
④

如图,点 是平行四边形 的边 上一点,且 .
(1)作出 的平分线,交 于点 (尺规作图,不写作法,保留作图痕迹);
(2)连接 ,求证:四边形 是菱形.

在2016年4月23日“世界读书日”之前,某校为了了解学生的阅读情况,对学生在2015年读课外书的数量进行了调查.所示图表是根据随机抽取的部分学生的读书数量情况整理的表格和两幅不完整的统计图,根据图中提供的信息,解答下列问题.
2015年学生的读书数量分组 |
||||
|
|
|
|
|
0 |
本 |
本 |
本 |
超过12本 |
(1)此次抽样调查共调查了 名学生?
(2)请将条形统计图补充完整;
(3)请说明样本数据中,学生读书数量的中位数落在哪个范围内;
(4)该校共有900名学生,估计在2015年读课外书的数量超过12本的学生有多少名?

某同学报名参加校运动会,有以下4个项目可选择.
径赛项目: 跑, 跑, 跑(分别用 , , 表示. 田赛项目:跳远(用 表示).
(1)该同学从4个项目中任选1个是径赛项目的概率为 .
(2)该同学从4个项目中任选2个,请用画树状图或列表的方法列举出所有可能出现的结果,并求参赛项目都是径赛的概率.
如图,一次函数 的图象与反比例函数 的图象在第二象限交于点 ,过点 作 轴于点 ,一次函数的图象分别交 、 轴于点 、 , ,
(1)求点 的坐标;
(2)求一次函数与反比例函数的表达式;
(3)根据图象直接写出不等式 的解集.

如图,这是一座一侧有缓步台的过街天桥示意图.已知桥面 长为 ,与水平面的垂直距离为 ,桥面 长为 ,与水平面的垂直距离为 .斜坡 , 与水平面的夹角分别为 , ,斜坡 的坡度(即 为 .求天桥跨度 的长.
参考数据: , ,

如图,在 中, ,以 为直径的 交 于点 ,且点 是 的中点,连接 交 于点 ,连接 , .
(1)求证: ;
(2)若 , ,求 的长.

某手工编织厂生产一种旅游纪念品,现有60名工人进行手工编织(每人编织的效率相同),2天后抽出10名工人执行其他任务,其余工人继续编织生产;2天后从编织的工人中再抽出10名进行销售(每人每天的销售量相同).已知每人每天的销售量是编织量的5倍,下图是产品库存量 (件 与生产时间 (天 之间的函数关系图象.
(1)解释点 的实际意义;
(2)求每人每天的编织量和销售量;
(3)求 段所在的直线的函数表达式,并求出多少天后剩余库存量低于生产前的库存量.

如图,在 中, ,点 从点 向点 运动,点 从点 沿射线 方向运动,且 ,连接 交 于 .
(1)如图1,当 时,求证: ;
(2)如图2,当 时,① , ,则 ;
②过点 作 于点 ,探究线段 , , 之间的数量关系,直接写出结论,不需证明.

如图,在平面直角坐标系中,二次函数 的图象经过平行四边形 的顶点 , 轴,垂足为点 .点 在 轴正半轴上,点 在 轴负半轴上,点 在 轴正半轴上,且 .

(1)求二次函数的表达式,并判断点 是否在该函数图象上;
(2)点 是线段 上一点,在线段 下方作 .
①当点 运动时,使 的一边 始终过点 ,另一边 交射线 于点 ,(不含点 与 重合的情形)设 , ,求 关于 的函数关系式,并求出 的取值范围.
②当 时,将 绕点 旋转,一条边 交线段 于点 ,另一条边 交线段 于点 ,连接 ,以 为直径作 ,设圆心 的坐标为 ,求 与 之间的函数关系式,并直接写出点 从点 运动到点 时圆心 运动的路径长.

 B.
B.
 D.
D.

 B.
B.
 D.
D.


 粤公网安备 44130202000953号
粤公网安备 44130202000953号