如图, 与 的边 相切,切点为 .将 绕点 按顺时针方向旋转得到△ ,使点 落在 上,边 交线段 于点 .若 ,则
度.
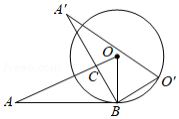
如图.将菱形 绕点 逆时针旋转 得到菱形 , .当 平分 时, 与 满足的数量关系是
| A. |
|
B. |
|
C. |
|
D. |
|
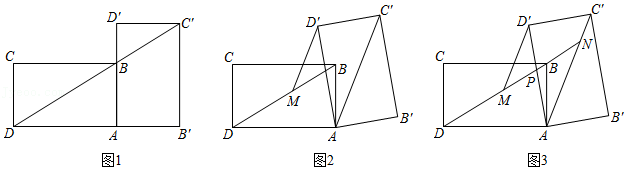
如图,在 的方格纸中,线段 的端点均在格点上,请按要求画图.

(1)如图1,画出一条线段 ,使 , 在格点上;
(2)如图2,画出一条线段 ,使 , 互相平分, , 均在格点上;
(3)如图3,以 , 为顶点画出一个四边形,使其是中心对称图形,且顶点均在格点上.
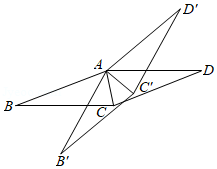
小王在学习浙教版九上课本第72页例2后,进一步开展探究活动:将一个矩形 绕点 顺时针旋转 ,得到矩形 ,连结 .
探究 如图1,当 时,点 恰好在 延长线上.若 ,求 的长.
探究 如图2,连结 ,过点 作 交 于点 .线段 与 相等吗?请说明理由.
探究 在探究2的条件下,射线 分别交 , 于点 , (如图 ,发现线段 , , 存在一定的数量关系,请写出这个关系式,并加以证明.
如图,已知正方形 边长为1, 为 边上一点,以点 为中心,将 按逆时针方向旋转得 ,连接 ,分别交 , 于点 , .若 ,则 .

如图,在 中, ,将 绕点 逆时针旋转得到 ,点 , 的对应点分别为 , ,连接 .当点 , , 在同一条直线上时,下列结论一定正确的是

| A. |
|
B. |
|
C. |
|
D. |
|
如图,在每个小正方形的边长为1个单位的网格中, 的顶点均在格点(网格线的交点)上.
(1)将 向右平移5个单位得到△ ,画出△ ;
(2)将(1)中的△ 绕点 逆时针旋转 得到△ ,画出△ .
如图,将 绕点 顺时针旋转 得到△ ,已知 , ,则线段 扫过的图形(阴影部分)的面积为 .

在等腰 中, ,点 是 边上一点(不与点 、 重合),连结 .
(1)如图1,若 ,点 关于直线 的对称点为点 ,连结 , ,则 ;
(2)若 ,将线段 绕点 顺时针旋转 得到线段 ,连结 .
①在图2中补全图形;
②探究 与 的数量关系,并证明;
(3)如图3,若 ,且 .试探究 、 、 之间满足的数量关系,并证明.

如图是由4个相同的小正方体堆成的物体,将它在水平面内顺时针旋转 后,其主视图是
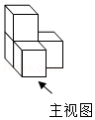
| A. |
|
B. |
|
C. |
|
D. |
|
下列图形均表示医疗或救援的标识,其中既是轴对称图形又是中心对称图形的是
| A. |
|
B. |
|
| C. |
|
D. |
|
如图,将△ ABC绕点 A逆时针旋转55°得到△ ADE,若 且 于点 F,则∠ BAC的度数为( )

| A. |
65° |
B. |
70° |
C. |
75° |
D. |
80° |
如图,在平面直角坐标系中, 的顶点坐标分别是 , , .
(1)将 以 为旋转中心旋转 ,画出旋转后对应的△ ;
(2)将 平移后得到△ ,若点 的对应点 的坐标为 ,求△ 的面积.
