初中数学图形的剪拼试题

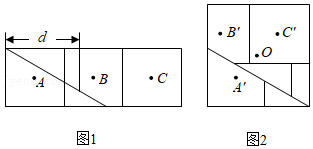
图1是邻边长为2和6的矩形，它由三个小正方形组成，将其剪拼成不重叠、无缝隙的大正方形（如图 $2)$ ，则图1中所标注的 $d$ 的值为 　　；记图1中小正方形的中心为点 $A$ ， $B$ ， $C$ ，图2中的对应点为点 $A\text{'}$ ， $B\text{'}$ ， $C\text{'}$ ．以大正方形的中心 $O$ 为圆心作圆，则当点 $A\text{'}$ ， $B\text{'}$ ， $C\text{'}$ 在圆内或圆上时，圆的最小面积为 　　．

将一张圆形纸片（圆心为点 $O)$沿直径 $\mathit{MN}$对折后，按图1分成六等份折叠得到图2，将图2沿虚线 $\mathit{AB}$剪开，再将 $\mathit{\Delta AOB}$展开得到如图3的一个六角星．若 $\angle \mathit{CDE}=75°$，则 $\angle \mathit{OBA}$的度数为 　　．

七巧板起源于我国先秦时期，古算书《周髀算经》中有关于正方形的分割术，经历代演变而成七巧板，如图1所示 $.19$ 世纪传到国外，被称为"唐图"（意为"来自中国的拼图" $)$ ，图2是由边长为4的正方形分割制作的七巧板拼摆而成的"叶问蹬"图，则图中抬起的"腿"（即阴影部分）的面积为 $($ 　　 $)$

A．

3

B．

$\frac{7}{2}$

C．

2

D．

$\frac{5}{2}$

小明有一个呈等腰三角形的积木盒，现在积木盒中只剩下如图的九个空格，下面有四种积木的搭配，其中不能放入的有 $($ 　　 $)$

A．

搭配①

B．

搭配②

C．

搭配③

D．

搭配④

综合实践活动课上，小亮将一张面积为 $24c{m}^2$ ，其中一边 $\mathit{BC}$ 为 $8\mathit{cm}$ 的锐角三角形纸片（如图 $1)$ ，经过两刀裁剪，拼成了一个无缝隙、无重叠的矩形 $\mathit{BCDE}$ （如图 $2)$ ，则矩形的周长为 　　 $\mathit{cm}$ ．

在我们学习过的数学教科书中，有一个数学活动，若身旁没有量角器或三角尺，又需要作 $60°$ ， $30°$ ， $15°$ 等大小的角，可以采用如下方法：

操作感知：

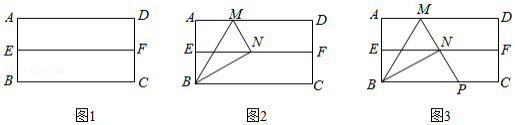
第一步：对折矩形纸片 $\mathit{ABCD}$ ，使 $\mathit{AD}$ 与 $\mathit{BC}$ 重合，得到折痕 $\mathit{EF}$ ，把纸片展开（如图1 $)$ ．

第二步：再一次折叠纸片，使点 $A$ 落在 $\mathit{EF}$ 上，并使折痕经过点 $B$ ，得到折痕 $\mathit{BM}$ ，同时得到线段 $\mathit{BN}$ （如图 $2)$ ．

猜想论证：

（1）若延长 $\mathit{MN}$ 交 $\mathit{BC}$ 于点 $P$ ，如图3所示，试判定 $\mathit{\Delta BMP}$ 的形状，并证明你的结论．

拓展探究：

（2）在图3中，若 $\mathit{AB}=a$ ， $\mathit{BC}=b$ ，当 $a$ ， $b$ 满足什么关系时，才能在矩形纸片 $\mathit{ABCD}$ 中剪出符合（1）中结论的三角形纸片 $\mathit{BMP}$ ？

如图所示的图案由三个叶片组成，绕点 $O$ 旋转 $120°$ 后可以和自身重合．若每个叶片的面积为 $4c{m}^2$ ， $\angle \mathit{AOB}$ 为 $120°$ ，则图中阴影部分的面积之和为 　　 $c{m}^2$ ．

课本再现

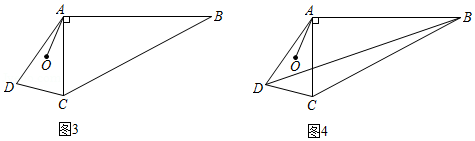
（1）在证明"三角形内角和定理"时，小明只撕下三角形纸片的一个角拼成图1即可证明，其中与 $\angle A$ 相等的角是 　　；

类比迁移

（2）如图2，在四边形 $\mathit{ABCD}$ 中， $\angle \mathit{ABC}$ 与 $\angle \mathit{ADC}$ 互余，小明发现四边形 $\mathit{ABCD}$ 中这对互余的角可类比（1）中思路进行拼合：先作 $\angle \mathit{CDF}=\angle \mathit{ABC}$ ，再过点 $C$ 作 $\mathit{CE}\perp \mathit{DF}$ 于点 $E$ ，连接 $\mathit{AE}$ ，发现 $\mathit{AD}$ ， $\mathit{DE}$ ， $\mathit{AE}$ 之间的数量关系是 　　；

方法运用

（3）如图3，在四边形 $\mathit{ABCD}$ 中，连接 $\mathit{AC}$ ， $\angle \mathit{BAC}=90°$ ，点 $O$ 是 $\mathit{\Delta ACD}$ 两边垂直平分线的交点，连接 $\mathit{OA}$ ， $\angle \mathit{OAC}=\angle \mathit{ABC}$ ．

①求证： $\angle \mathit{ABC}+\angle \mathit{ADC}=90°$ ；

②连接 $\mathit{BD}$ ，如图4，已知 $\mathit{AD}=m$ ， $\mathit{DC}=n$ ， $\frac{\mathit{AB}}{\mathit{AC}}=2$ ，求 $\mathit{BD}$ 的长（用含 $m$ ， $n$ 的式子表示）．

如图是用七巧板拼接成的一个轴对称图形（忽略拼接线）小亮改变①的位置，将①分别摆放在图中左，下，右的位置（摆放时无缝隙不重叠），还能拼接成不同轴对称图形的个数为 $($ 　　 $)$

A．

2

B．

3

C．

4

D．

5

中国古代数学家刘徽在《九章算术注》中，给出了证明三角形面积公式的出入相补法．如图所示，在 $\mathit{\Delta ABC}$ 中，分别取 $\mathit{AB}$ 、 $\mathit{AC}$ 的中点 $D$ 、 $E$ ，连接 $\mathit{DE}$ ，过点 $A$ 作 $\mathit{AF}\perp \mathit{DE}$ ，垂足为 $F$ ，将 $\mathit{\Delta ABC}$ 分割后拼接成矩形 $\mathit{BCHG}$ ．若 $\mathit{DE}=3$ ， $\mathit{AF}=2$ ，则 $\mathit{\Delta ABC}$ 的面积是 　　．

在综合实践课上，老师要求同学用正方形纸片剪出正三角形且正三角形的顶点都在正方形边上．小红利用两张边长为2的正方形纸片，按要求剪出了一个面积最大的正三角形和一个面积最小的正三角形．则这两个正三角形的边长分别是 　　．

七巧板是我们祖先的一项创造，被誉为“东方魔板”．在一次数学活动课上，小明用边长为 $4\mathit{cm}$的正方形纸片制作了如图所示的七巧板，并设计了下列四幅作品 $--$ “奔跑者”，其中阴影部分的面积为 $5c{m}^2$的是 $($　　 $)$

A．B．

C．D．

如图，四边形 $\mathit{ABCD}$ 是一张平行四边形纸片，其高 $\mathit{AG}=2\mathit{cm}$ ，底边 $\mathit{BC}=6\mathit{cm}$ ， $\angle B=45°$ ，沿虚线 $\mathit{EF}$ 将纸片剪成两个全等的梯形，若 $\angle \mathit{BEF}=30°$ ，则 $\mathit{AF}$ 的长为 $($ 　　 $)$

A．

$1\mathit{cm}$

B．

$\frac{\sqrt{6}}{3}\mathit{cm}$

C．

$(2\sqrt{3}-3)\mathit{cm}$

D．

$(2-\sqrt{3})\mathit{cm}$

用四块大正方形地砖和一块小正方形地砖拼成如图所示的实线图案，每块大正方形地砖面积为 $a$，小正方形地砖面积为 $b$，依次连接四块大正方形地砖的中心得到正方形 $\mathit{ABCD}$．则正方形 $\mathit{ABCD}$的面积为　　．（用含 $a$， $b$的代数式表示）

如图，等边三角形纸片 $\mathit{ABC}$的边长为6， $E$， $F$是边 $\mathit{BC}$上的三等分点．分别过点 $E$， $F$沿着平行于 $\mathit{BA}$， $\mathit{CA}$方向各剪一刀，则剪下的 $\mathit{\Delta DEF}$的周长是　　．