七巧板起源于我国先秦时期,古算书《周髀算经》中有关于正方形的分割术,经历代演变而成七巧板,如图1所示 世纪传到国外,被称为"唐图"(意为"来自中国的拼图" ,图2是由边长为4的正方形分割制作的七巧板拼摆而成的"叶问蹬"图,则图中抬起的"腿"(即阴影部分)的面积为

| A. |
3 |
B. |
|
C. |
2 |
D. |
|
小明有一个呈等腰三角形的积木盒,现在积木盒中只剩下如图的九个空格,下面有四种积木的搭配,其中不能放入的有

| A. |
搭配① |
B. |
搭配② |
C. |
搭配③ |
D. |
搭配④ |
如图是用七巧板拼接成的一个轴对称图形(忽略拼接线)小亮改变①的位置,将①分别摆放在图中左,下,右的位置(摆放时无缝隙不重叠),还能拼接成不同轴对称图形的个数为

| A. |
2 |
B. |
3 |
C. |
4 |
D. |
5 |
七巧板是我们祖先的一项创造,被誉为“东方魔板”.在一次数学活动课上,小明用边长为 的正方形纸片制作了如图所示的七巧板,并设计了下列四幅作品 “奔跑者”,其中阴影部分的面积为 的是

A. B.
B.
C. D.
D.
如图,四边形 是一张平行四边形纸片,其高 ,底边 , ,沿虚线 将纸片剪成两个全等的梯形,若 ,则 的长为

| A. |
|
B. |
|
C. |
|
D. |
|
七巧板是我国祖先的一项卓越创造,流行于世界各地.由边长为2的正方形可以制作一副中国七巧板或一副日本七巧板,如图1所示.分别用这两副七巧板试拼如图2中的平行四边形或矩形,则这两个图形中,中国七巧板和日本七巧板能拼成的个数分别是

A.1和1B.1和2C.2和1D.2和2
如图,正方形硬纸片 的边长是4,点 、 分别是 、 的中点,若沿左图中的虚线剪开,拼成如图的一座“小别墅”,则图中阴影部分的面积是

A.2B.4C.8D.10
一个大矩形按如图方式分割成九个小矩形,且只有标号为①和②的两个小矩形为正方形,在满足条件的所有分割中.若知道九个小矩形中 个小矩形的周长,就一定能算出这个大矩形的面积,则 的最小值是
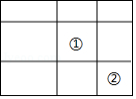
A.3B.4C.5D.6
七巧板是我国祖先的一项卓越创造.下列四幅图中有三幅是小明用如图所示的七巧板拼成的,则不是小明拼成的那副图是

A.
B.
C.
D.
观察下列各方格图中阴影部分所示的图形(每一小方格的边长为 ,如果将它们沿方格边线或对角线剪开重新拼接,不能拼成正方形的是
A. B.
B.
C. D.
D.
如图1,分别沿长方形纸片 和正方形纸片 的对角线 , 剪开,拼成如图2所示的 ,若中间空白部分四边形 恰好是正方形,且 的面积为50,则正方形 的面积为

| A. |
24 |
B. |
25 |
C. |
26 |
D. |
27 |
如图,矩形纸片 中, , .将该矩形纸片剪去3个等腰直角三角形,所有剪法中剩余部分面积的最小值是

A.6B.3C.2.5D.2
如图是用8块 型瓷砖(白色四边形)和8块 型瓷砖(黑色三角形)不重叠、无空隙拼接而成的一个正方形图案,图案中 型瓷砖的总面积与 型瓷砖的总面积之比为

| A. |
|
B. |
|
C. |
|
D. |
|
在数学拓展课上,小明发现:若一条直线经过平行四边形对角线的交点,则这条直线平分该平行四边形的面积.如图是由5个边长为1的小正方形拼成的图形, 是其中4个小正方形的公共顶点,小强在小明的启发下,将该图形沿着过点 的某条直线剪一刀,把它剪成了面积相等的两部分,则剪痕的长度是

| A. |
|
B. |
|
C. |
|
D. |
|