已知一根质量分布均匀的圆柱体木料质量为 ,体积为 。问:
(1)此木料的密度为多少?
(2)如图所示,甲、乙两人分别在 点和 点共同扛起此木料并恰好水平,其中 , 为木料的中点。求此时乙对木料的作用力大小。
(3)若在(2)中当乙的作用点从 点向 点靠近时,请列式分析此过程中甲对木料作用力大小变化情况。

水平桌面上有一底面积为 的圆柱形薄壁容器,容器内装有一定质量的水。将底面积为 、高为 的柱形杯装满水后(杯子材料质地均匀),竖直放入水中,静止后容器中水的深度为 ,如图1所示;再将杯中的水全部倒入容器内,把空杯子竖直正立放入水中,待杯子自由静止后,杯底与容器底刚好接触,且杯子对容器底的压力为零,容器中水的深度为 ,如图2所示。已知水的密度为 。求:
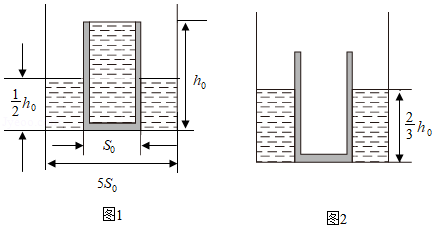
(1)空杯子的质量;
(2)该杯子材料的密度。
如图甲所示,一轻质弹簧,其两端分别固定在容器底部和正方体物块上。已知物块的边长为10cm,弹簧没有发生形变时的长度为15cm,弹簧受到拉力作用后,伸长的长度ΔL与拉力F的关系如图乙所示。向容器中加水,直到物块上表面与水面相平,此时水深30cm。
(1)该物块受到水的浮力;
(2)该物块的密度;
(3)打开出水口,缓慢放水,当弹簧恢复原状时,关闭出水口。求放水前后水对容器底部压强的变化量。

如图甲所示,一边长为10cm的正方体物块漂浮于足够高、底面积为0.02m 2的盛有足量水的圆柱形容器中,有 体积露出水面,ρ 水=1.0×10 3kg/m 3,g取10N/kg。求:
(1)该物块受到的浮力;
(2)物块的密度。

如图所示,质量为10kg,底面积为500cm 2的圆柱体A放在水平面上。一薄壁圆柱形容器B也置于水平面上,该容器足够高,底面积为200cm 2,内盛有8kg的水。若将一物体M分别放在圆柱体A上表面的中央和浸没在容器B的水中时,圆柱体A对水平面的压强变化量和水对容器B底部压强的变化量相等(g取10N/kg,ρ 水=1.0×10³kg/m³),则( )

| A. |
未放上物体M时,圆柱体A对水平地面的压强为2×10 5Pa |
| B. |
容器B内水的体积为0.08m³ |
| C. |
物体M的密度为2.5×10³kg/m³ |
| D. |
物体M未放入容器B时,容器B底部受到的水的压强为4×10 4Pa |
如图所示是一个水位监测仪的简化模型。杠杆 质量不计, 端悬挂着物体 , 端悬挂着物体 ,支点为 , 。物体 下面是一个压力传感器,物体 是一个质量分布均匀的实心圆柱体,放在水槽中,当水槽中无水时,物体 下端与水槽的底部恰好接触且压力为零,此时压力传感器的示数也为零。已知物体 的质量 ,高度 ,横截面积 取 , 。求:
(1)物体 的密度 ;
(2)物体 的质量 ;
(3)当压力传感器的示数 时,求水槽内水的深度 。

如图甲是西南大学校内的一座塑像,其基座结构类似于图乙和丙的模型。若 、 是质量分布均匀地正方体物块,其边长分别是 、 ,密度之比 .将 放在水平地面上, 放在 的上面, 对水平地面的压强为 (如图乙)。求:
(1)图乙中,物块 对地面的压力;
(2)物块 的密度;
(3)若将物块 放在水平地面上, 放在 的上面(如图丙),要使 对地面的压强为 ,应将物块 沿竖直方向切去几分之几。
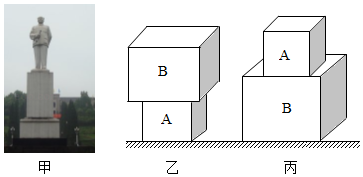
“童话云和”盛产木制玩具,是著名的木玩之城。小科同学从某玩具厂得到三块相同的积木,利用该积木和简单的器材在家里进行了“科学小实验”。请分析回答:
(1)称得一块积木的质量为144克,测得该积木的长10厘米、宽6厘米、高4厘米,则积木的密度为 克 厘米 ;
(2)当将积木搭成如图三种方式时,积木对水平地面的压强大小关系为 (用 、 、 表示);
(3)把一块积木放入水中,若要使积木的上表面恰好浸没,则在积木上至少要施加多大的力?

如图甲所示,水平桌面上有个质量为 ,底面边长为 的正方体水槽,水槽内有一实心球。逐渐往水槽内加水,球受到的浮力 与水深 的关系如图乙所示,水深 时,球刚好有一半体积浸入水中。不考虑水槽厚度,水的密度为 ,求:
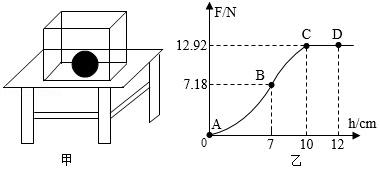
(1)实心球的体积和水深 时水槽底部受到的水的压强;
(2)实心球的密度;
(3)实心球刚好离开水槽底部时水槽对水平桌面的压强。
质量为 的科考潜水器,在水下匀速下潜或加速下潜时受到水的阻力各不相同。若潜水器下潜时所受阻力与速度的关系如下表:
|
速度 |
1.2 |
1.2 |
1.2 |
1.3 |
1.4 |
1.5 |
1.6 |
1.7 |
|
阻力 |
300 |
300 |
300 |
320 |
340 |
360 |
380 |
400 |
求:(1)潜水器在水面下 处,受到水的压强为多少?(水的密度为
(2)向潜水器水仓中注入 水后,潜水器刚好以 的速度匀速下潜,求注水后潜水器的平均密度。
(3)写出潜水器加速下潜时,所受阻力 与速度 的关系式: 。
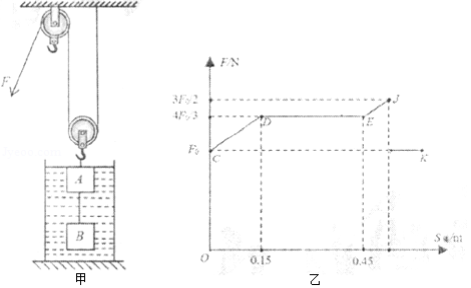
如图甲所示, 、 为不同材料制成的体积相同的实心正方体,浸没在圆柱形容器的水中,容器内部底面积是正方体下表面积的4倍。沿固定方向缓慢匀速拉动绳子,开始时刻, 的上表面刚好与水面相平,滑轮组绳子自由端的拉力 大小为 , 随绳端移动距离 变化的图象如图乙所示。已知动滑轮的重力 , 取 。除了连接 、 间的绳子承受拉力有一定限度外,其它绳子都不会被拉断。滑轮与轴的摩擦、绳的质量等次要因素都忽略不计。
(1)正方体 、 之间的绳子长度 是多少?
(2)正方体 和 的密度 、 分别是多少?
(3)整个过程中,水对容器底部压强的最大变化量△ 是多少?
如图甲所示是使用汽车打捞水库中重物的示意图,汽车通过定滑轮牵引水下一个质量均匀分布的正方体重物,在整个打捞过程中,汽车以恒定的速度 向右运动。图乙是此过程中汽车拉力 跟时间 变化的图象。设 时汽车开始提升重物,忽略水的阻力和滑轮的摩擦, 取 。求:
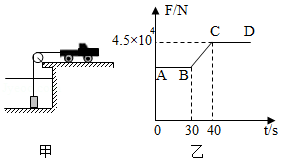
(1)水库水的深度;
(2)重物的密度。
(3)整个打捞过程中汽车的最小功率。
如图所示,水平桌面上放置一圆柱形容器,其内底面积为 ,容器侧面靠近底部的位置有一个由阀门 控制的出水口,物体 是边长为 的正方体,用不可伸长的轻质细线悬挂放入水中静止,此时有 的体积露出水面,细线受到的拉力为 ,容器中水深为 。已知,细线能承受的最大拉力为 ,细线断裂后物体 下落过程不翻转,物体 不吸水, 取 。
(1)求物体 的密度;
(2)打开阀门 ,使水缓慢流出,问放出大于多少 水时细线刚好断裂?
(3)细线断裂后立即关闭阀门 ,关闭阀门 时水流损失不计,物体 下落到容器底部稳定后,求水对容器底部的压强;
(4)从细线断裂到物体 下落到容器底部的过程中,求重力对物体 所做的功。

如图所示是某型起吊装置示意图。在某次打捞过程中,使用该装置将质量为 的水中物体 在 的时间内匀速竖直吊起 高(物体 未露出水面),电动机工作电压为 ,工作电流为 ,电动机对钢绳的拉力 为 ,滑轮组的机械效率为 ,已知水的密度为 .求:
电动机在 内消耗的电能;
(2)钢绳拉力 在 内做的功;
(3)物体 所受拉力 的大小;
(4)物体 的密度。
