初中数学解答题

如图，双曲线上点A的坐标为（1，2），过点A的直线y=x+b交x轴于点M，交y轴于点N，过A作AP⊥x轴于点P。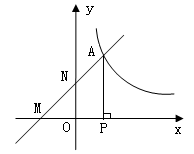

分别求k、b的值；
求△AMP的周长。

某检测小组乘汽车检修供电线路，约定向东方向出发为正，向西方向出发为负，某天检测小组自A地出发到收工时，行驶情况（单位：km）为：+22，-3，+4，-2，-8，+17，-2，-3，+12，+7，-5 .
收工时车辆停在何处？
若每千米耗油0.2升，从A地出发到收工共耗油多少升？

将下列各数按从小到大的顺序排列，用“<”号连结起来（本小题2分）
、 、 、 、  、 

利民种子培育基地用A、B、C三种型号的玉米种子共1500粒进行发芽试验，从中选出发芽率高的种子进行推广．通过试验知道，C型号种子的发芽率为80%，根据试验数据绘制了下面两个不完整的统计图(图1、图2)：
C型号种子的发芽数是_________粒；
通过计算说明，应选哪种型号的种子进行推广？(精确到1%)
如果将所有已发芽的种子放到一起，从中随机取出一粒，求取到C型号发芽种子的概率．

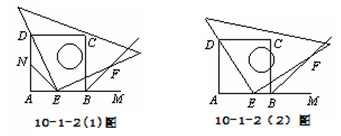
如图10－1－2（1），10－1－2（2），四边形ABCD是正方形，M是AB延长线上一点。直角三角尺的一条直角边经过点D，且直角顶点E在AB边上滑动（点E不与点A，B重合），另一条直角边与∠CBM的平分线BF相交于点F。
如图10－1－2（1），当点E在AB边的中点位置时：
①通过测量DE，EF的长度，猜想DE与EF满足的数量关系是         ；
②连接点E与AD边的中点N，猜想NE与BF满足的数量关系是             ；
③请证明你的上述两猜想。
如图10－1－2（2），当点E在AB边上的任意位置时，请你在AD边上找到一点N，使得NE=BF，进而猜想此时DE与EF有怎样的数量关系。

① 存在两个不同的无理数, 它们的积是整数； ② 存在两个不同的无理数, 它们的差是非零整数； ③ 存在两个不同的非整数的有理数, 它们的和与商都是整数. 先判断这3个结论分别是正确还是错误的, 如果正确, 请举出符合结论的两个数.

如图，有一个直角三角形纸片，两直角边AC=6cm,BC=8cm,现将直角边AC沿∠CAB
的角平分线AD折叠，使它落在斜边AB上，且与AE重合，你能求出CD的长吗？

 

一个角的补角比它的余角的2倍大64 º，求这个角的度数。

在半径为10的圆的铁片中，要裁剪出一个直角扇形，求能裁剪出的最大的直角扇形的面积？

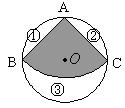
若用这个最大的直角扇形恰好围成一个圆锥，求这个圆锥的底面圆的半径？
能否从最大的余料③中剪出一个圆做该圆锥的底面？请说明理由．

如图，用直尺和圆规作出△ABC的外接圆⊙O (不写作法，保留作图痕迹)

若∠ABC=110°，求∠AOC的度数

已知：AB＝CD，AE⊥BC于E，DF⊥BC于F，且CE＝BF 。  
求证：AB∥CD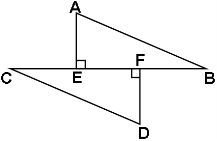

先化简式子(－)÷，然后请选取一个你最喜欢的x值代入求出这个式子的值.

现有大小两艘轮船，小船每天运 x吨货物，大船比小船每天多运10吨货物．现在让大船完成运送100吨货物的任务，小船完成运送80吨货物的任务
分别写出大船、小船完成任务用的时间？
试说明哪艘轮船完成任务用的时间少？

先观察下图的立体图形，再分别画出从它的正面、左面、上面三个方向所看到的平面图形.

若函数y＝kx+b的图像经过点（－3，－2）和（1，6）求k、b及函数关系式。