初中数学计算题

如图，直线y=-x+2与x轴交于点B，与y轴交于点C，已知二次函数的图象经过点B，C和点A（-1，0）．

（1）求B，C两点坐标；
（2）求该二次函数的关系式；
（3）若抛物线的对称轴与x轴的交点为点D，点E是线段BC上的一个动点，过点E作x轴的垂线与抛物线相交于点F，当点E运动到什么位置时，四边形CDBF的面积最大？求出四边形CDBF的最大面积及此时E点的坐标；
（4）在抛物线的对称轴上是否存在点P，使△PCD是以CD为腰的等腰三角形？如果存在，直接写出P点的坐标；如果不存在，请说明问题．

计算：．

计算：（每小题5分，共20分）
（1）；
（2）；
（3）；
（4）．

在下图中用阴影部分表示公顷。

①在下列圆中画一个最大的正方形。
②如果圆的直径是6cm，那么这个正方形的面积是（）cm²。

甲数的等于乙数的，乙数是60，甲数是多少？

100﹣98+96﹣94+92﹣90+…+76﹣74+72=

计算（能简算的要简算，每小题3分，共15分。）
（1）56×（+﹣）
（2）8.32×101﹣8.32
（3）6.75﹣+3.25﹣
（4）÷[×（+）]
（5）（﹣）÷（+）

（本小题满分12分）如图，在直角坐标系xOy中，一次函数（m为常数）的图像与x轴交于A（-3，0），与y轴交于点C；以直线为对称轴的抛物线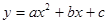（a，b，c为常数，且a＞0）经过A，C两点，与x轴正半轴交于点B．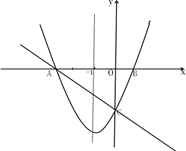

（1）求一次函数及抛物线的函数表达式。
（2）在对称轴上是否存在一点P，使得PBC的周长最小，若存在，请求出点P的坐标．
（3）点D是线段OC上的一个动点（不与点O、点C重合），过点D作DE‖PC交x轴于点E，连接PD、PE。设CD的长为m， PDE的面积为S。求S与m之间的函数关系式。并说明S是否存在最大值，若存在，请求出最大值：若不存在，请说明理由。

（本题13分）如图，抛物线y= -x²+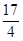x+1与y轴交于A点，过点A的直线与抛物线交于另一点B，过点B作BC⊥x轴，垂足为点C（3，0）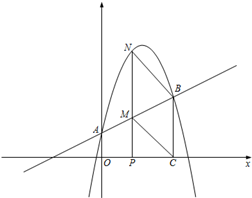

（1）求直线AB的函数关系式；
（2）动点P在线段OC上从原点出发以每秒一个单位的速度向C移动，过点P作PN⊥x轴，交直线AB于点M，交抛物线于点N．设点P移动的时间为t秒，MN的长度为s个单位，求s与t的函数关系式，并写出t的取值范围；
（3）设在（2）的条件下（不考虑点P与点O，点C重合的情况），连接CM，BN，当t为何值时，四边形BCMN为平行四边形？问对于所求的t值，平行四边形BCMN是否菱形？请说明理由．

（14 分）如图，在矩形OABC 中，OA=5，AB=4，点D 为边AB 上一点，将△BCD 沿直线CD 折叠，使点B 恰好落在OA边上的点E 处，分别以OC，OA 所在的直线为x 轴，y 轴建立平面直角坐标系．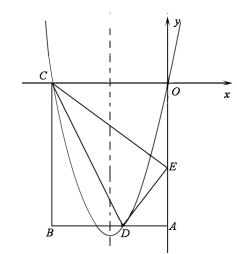

（1）求OE 的长；
（2）求经过O，D，C 三点的抛物线的解析式；
（3）一动点P 从点C 出发，沿CB 以每秒2 个单位长的速度向点B 运动，同时动点Q 从E 点出发，沿EC 以每秒1 个单位长的速度向点C 运动，当点P 到达点B 时，两点同时停止运动．设运动时间为t 秒，当t为何值时，DP=DQ；
（4）若点N 在（2）中的抛物线的对称轴上，点M 在抛物线上，是否存在这样的点M与点N，使得以M，N，C，E 为顶点的四边形是平行四边形？若存在，请求出M 点的坐标；若不存在，请说明理由．

化简下列各式：
（1）；
（2）．

如图1，已知∠DAC=90°，△ABC是等边三角形，点P为射线AD上任意一点（点P与点A不重合），连结CP，将线段CP绕点C顺时针旋转60°得到线段CQ，连结QB并延长交直线AD于点E．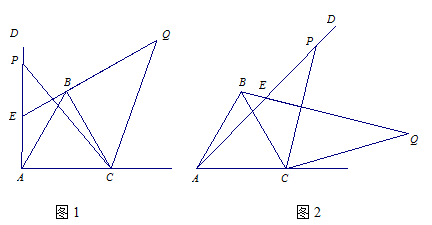

（1）如图1，猜想∠QEP=°；
（2）如图2，3，若当∠DAC是锐角或钝角时，其它条件不变，猜想∠QEP的度数，选取一种情况加以证明；
（3）如图3，若∠DAC=135°，∠ACP=15°，且AC=4，求BQ的长．

（每小题3分，共6分）计算：
（1）
（2）

（5’）（1）计算：
（5’）（2）解不等式组．