已知函数 的图象如图所示,以下结论:①m<0;②在每个分支上y随x的增大而增大;③若点A(-1,a)、点B(2,b)在图象上,则a<b;④若点P(x,y)在图象上,则点P1(-x,-y)也在图象上.其中正确的个数是( )
的图象如图所示,以下结论:①m<0;②在每个分支上y随x的增大而增大;③若点A(-1,a)、点B(2,b)在图象上,则a<b;④若点P(x,y)在图象上,则点P1(-x,-y)也在图象上.其中正确的个数是( )
| A.4个 | B.3个 | C.2个 | D.1个 |
已知函数 的图象如图,有以下结论:
的图象如图,有以下结论:
①m<0;
②在每一个分支上,y随x的增大而增大;
③若点A(-1,a)、B(2,b)在图象上,则a<b;
④若点P(x,y)在图象上,则点P1(-x,-y)也在图象上.
其中正确结论的个数为( )
| A.4 | B.3 | C.2 | D.1 |
若变量m与n之间的函数解析式为 (a为不等于1的常数),则m是n的( )
(a为不等于1的常数),则m是n的( )
| A.一次函数 | B.正比例函数 |
| C.反比例函数 | D.无法确定 |
若 与y成反比例,
与y成反比例, 与z成正比例,则x与z所成的函数关系为( )
与z成正比例,则x与z所成的函数关系为( )
| A.正比例函数关系 | B.反比例函数关系 |
| C.不成比例关系 | D.一次函数关系 |
若函数y=2x+k的图象与x轴的正半轴相交,则函数 的图象位于( )
的图象位于( )
| A.第二、第三象限 | B.第三、第四象限 |
| C.第二、第四象限 | D.第一、第三象限 |
已知一次函数y=kx+b的图象如图所示,那么正比例函数y=kx和反比例函数 在同一平面直角坐标系中的图象大致是( )
在同一平面直角坐标系中的图象大致是( )
A. |
B. |
C. |
D. |
若变量m与n之间的函数解析式为 (a为不等于1的常数),则m是n的( )
(a为不等于1的常数),则m是n的( )
| A.一次函数 | B.正比例函数 |
| C.反比例函数 | D.无法确定 |
若 与y成反比例,
与y成反比例, 与z成正比例,则x与z所成的函数关系为( )
与z成正比例,则x与z所成的函数关系为( )
| A.正比例函数关系 |
| B.反比例函数关系 |
| C.不成比例关系 |
| D.一次函数关系 |
如图,在平面直角坐标系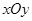 中,直线
中,直线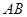 经过点
经过点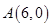 、
、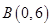 ,⊙
,⊙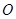 的半径为2(
的半径为2(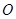 为坐标原点),点
为坐标原点),点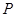 是直线
是直线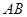 上的一动点,过点
上的一动点,过点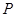 作⊙
作⊙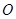 的一条切线
的一条切线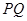 ,
,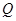 为切点,则切线长
为切点,则切线长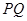 的最小值为( ).
的最小值为( ).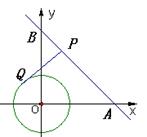
A.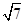 |
B.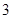 |
C.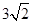 |
D.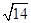 |
如图,点A、B、C、D、E、F、G、H、K都是7×8方格纸中的格点,为使△DEM ∽△ABC,则点M所在位置应是F、G、H、K四点中的( )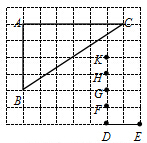
A.K B.H C.G D.F
如图,在矩形纸片ABCD中,AB=5CM,BC=10CM,CD上有一点E,ED=2cm,AD上有一点P,PD=3cm,过点P作PF⊥AD,交BC于点F,将纸片折叠,使点P与点E重合,折痕与PF交于点Q,则PQ的长是( ).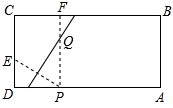
A.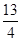 cm cm |
B.3cm | C.2cm | D.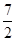 cm cm |
小芳步行上学,最初以某一速度匀速前进,中途遇红灯,稍作停留后加快速度跑步去上学,到校后,她请同学们画出她行进路程s(米)与行进时间t(分钟)的函数图象的示意图.你认为正确的是( )
随着生活水平的提高,小林家购置了私家车,这样他乘坐私家车上学比乘坐公交车上学所需的时间少用了15分钟,现已知小林家距学校8千米,乘私家车平均速度是乘公交车平均速度的2.5倍,若设乘公交车平均每小时走x千米,根据题意可列方程为( )
A.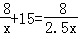 |
B.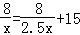 |
C.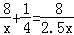 |
D.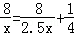 |
已知:如图,Rt△ABC中,∠BAC=90°,BC=13,AB=12,E是BC边上一点,过点E作DE⊥BC,交AC所在直线于点D,若BE=x,△DCE的面积为y,则y与x的函数图象大致是( )

A. |
B. |
C. |
D. |