已知⊙O1与⊙O2外切于点A,⊙O1的半径R=2,⊙O2的半径r=1,若半径为4的⊙C与⊙O1、⊙O2都相切,则满足条件的⊙C有( )
| A.2个 | B.4个 | C.5个 | D.6个 |
如图,平面直角坐标系中,⊙P与x轴分别交于A、B两点,点P的坐标为(3,-1),AB=2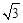 .若将⊙P向上平移,则⊙P与x轴相切时点P的坐标为 ;
.若将⊙P向上平移,则⊙P与x轴相切时点P的坐标为 ;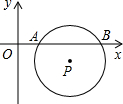
如图,等边三角形ABC内接于⊙O,那么∠BOC的度数是( )
| A.150° | B.120° | C.90° | D.60° |
如图,⊙ 的半径为2,点
的半径为2,点 到直线
到直线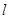 的距离为3,点
的距离为3,点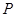 是直线
是直线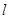 上的一个动点,
上的一个动点,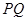 切⊙
切⊙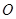 于点
于点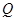 ,则
,则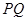 的最小值为 ( )
的最小值为 ( )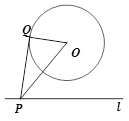
A.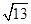 |
B.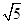 |
C.3 | D.5 |
如图,点C在⊙O上,若∠ACB=40°,则∠AOB等于( )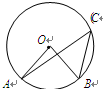
| A.40° | B.60° | C.80° | D.100° |
李老师在与同学进行“蚂蚁怎样爬最近”的课题研究时设计了以下三个问题,请你根据下列所给的重要条件分别求出蚂蚁需要爬行的最短路程的长.
(1)如图1,正方体的棱长为5cm一只蚂蚁欲从正方体底面上的点A沿着正方体表面爬到点C1处;
(2)如图2,圆锥的母线长为4cm,底面半径r= cm,一只蚂蚁欲从圆锥的底面上的点A出发,沿圆锥侧面爬行一周回到点A;
cm,一只蚂蚁欲从圆锥的底面上的点A出发,沿圆锥侧面爬行一周回到点A;
(3)如图3,是一个没有上盖的圆柱形食品盒,一只蚂蚁在盒外表面的A处,它想吃到盒内表面对侧中点B处的食物,已知盒高10cm,底面圆周长为32cm,A距下底面3cm..
如图,P是⊙O的直径AB延长线上的一点, PC切⊙O于点C,弦CD⊥AB,垂足为点E,若 ,
, .
.

求:(1)⊙O的半径;
(2)CD的长;
(3)图中阴影部分的面积.
如图所示,AB是⊙O的一条弦,OD⊥AB,垂足为C,交⊙O于点D,点E在⊙O上.
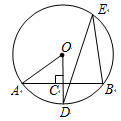
若∠AOD =52º,求∠DEB的度数;
若OC=3,OA=5,求AB的长.
如图,已知点A、B、C在⊙O上,∠COA=100°,则∠CBA的度数是( ). A.50° B.80° C.100° D.200°
A.50° B.80° C.100° D.200°
如图,AB为 的直径,AB=AC,BC交
的直径,AB=AC,BC交 于点D,AC交
于点D,AC交 于点E.
于点E.
(1)求证:BD=CD;
(2)若AB=8,∠BAC=45°,求阴影部分的面积.