2011-2012学年福建省福州市台江区九年级第一学期期中质检数学试卷
如图,点A、B、C、D、O都在方格纸的格点上,若△COD是由
△AOB绕点O按顺时针方向旋转而得,则旋转的角度是( ).
A.30° B.45° C.90° D.135°
如图是一张长8cm、宽5cm的矩形纸板,将纸板四个角各剪去一个同样的正方形,可制成底面积是18 的一个无盖长方体纸盒,设剪去的正方形边长为
的一个无盖长方体纸盒,设剪去的正方形边长为 ,那么
,那么 满足的方程是( ).
满足的方程是( ).
A. |
B. |
C. |
D. |

如图,在Rt△ABC中,∠ACB=90º,∠A=30º,BC=2,将△ABC 绕点C按顺时针方向旋转n度后,得到△EDC.当点D恰好落在在AB边上时,则n的大小和图中阴影部分的面积分别是( ).
A.30,2 B.60,2 C.60, D.60,
D.60,

如图,已知点A,B的坐标分别为(4,0),(3,2).
画出△AOB关于原点O对称的图形△COD;
将△AOB绕点O按逆时针方向旋转90°得到△EOF,画出△EOF;
点D的坐标是( ),点F的坐标是( ),此图中线段BF和DF的关系是 .
如图,直线AB经过⊙O上的点C,OA=OB,CA=CB.
直线AB是否与⊙O相切?为什么?
如果⊙O的直径为4cm,AB=8cm,求OA的长
某市为进一步创建宜居城市,2009年市政府对市区绿化工程投入的资金是2000
万元,2011年投入的资金是2420万元,设两年间每年投入资金的年平均增长率相同求该市对市区绿化工程投入资金的年平均增长率;
若该市对市区绿化工程投入资金的年平均增长率保持不变,预计2012年市政府对市区绿化工程投入的资金是多少万元?
关于 的一元二次方程
的一元二次方程 的一个根是2.
的一个根是2.求
 的值和方程的另一个根
的值和方程的另一个根
若直线AB经过点A(2,0),B(0,
 ),求直线AB的解析式;
),求直线AB的解析式;在平面直角坐标系中画出直线AB的图象,P是
 轴上一动点,是否存在点P,
轴上一动点,是否存在点P,
使△ABP是直角三角形,若存在,求出点P坐标,若不存在,说明理由.
如图1,在平面直角坐标系中,以坐标原点O为圆心的⊙O的半径为 ,
,
直线 :
: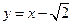 与坐标轴分别交于A、C两点,点B的坐标为(-4,1),⊙B与
与坐标轴分别交于A、C两点,点B的坐标为(-4,1),⊙B与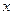
轴相切于点M.
求点A的坐标及∠CAO的度数
⊙B以每秒1个单位长度的速度沿
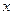 轴向右平移,同时,直线
轴向右平移,同时,直线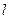 绕点A逆时针匀速旋转.当⊙B第一次与⊙O相切时,直线
绕点A逆时针匀速旋转.当⊙B第一次与⊙O相切时,直线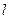 也恰好与⊙B第一次相切,问:直线
也恰好与⊙B第一次相切,问:直线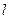 绕点A
绕点A
每秒旋转多少度?如图2,过A、O、C三点作⊙O1,点E为劣弧AO上一点,连接EC、EA、EO,
当点E在劣弧AO上运动时(不与A、O两点重合), 的值是否发生变化?如
的值是否发生变化?如
果不变,求其值;如果变化,说明理由.
 的结果是( ).
的结果是( ).
 的解是( ).
的解是( ).


 A.50° B.80° C.100° D.200°
A.50° B.80° C.100° D.200°



 的根的情况是( ).
的根的情况是( ). ,则PA+PB的最小值是( ).
,则PA+PB的最小值是( ).



 有意义,则
有意义,则 的取值范围是
的取值范围是 
 满足
满足 ,那么我们称这个方程为“凤凰方程”.已知
,那么我们称这个方程为“凤凰方程”.已知 是关于
是关于 的凤凰方程,
的凤凰方程, 是方程的一个根,
是方程的一个根,



 粤公网安备 44130202000953号
粤公网安备 44130202000953号