初中数学圆幂定理填空题

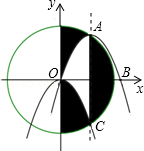
已知AB为⊙O的直径AC、AD为⊙O的弦，若AB=2AC=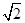AD，则∠DBC的度数为

如右图，正六边形ABCDEF的边长为2，两顶点A、B分别在x轴和y轴上运动，则顶点D到原点O的距离的最大值和最小值的乘积为．

如图所示中的∠A的正切值为．

如图，正方形的边长为2，以为圆心、为半径作弧交于点，设弧与边、围成的阴影部分面积为；然后以为对角线作正方形，又以为圆心、为半径作弧交于点，设弧与边、围成的阴影部分面积为；…，按此规律继续作下去，设弧与边、围成的阴影部分面积为．则：（1）=；（2）=．

把边长为1的正方形纸片OABC放在直线m上，OA边在直线m上，然后将正方形纸片绕着顶点A按顺时针方向旋转90°，此时，点O运动到了点O₁处（即点B处），点C运动到了点C₁处，点B运动到了点B₁处，又将正方形纸片AO₁C₁B₁绕B₁点，按顺时针方向旋转90°…，按上述方法经过4次旋转后，顶点O经过的总路程为，经过61次旋转后，顶点O经过的总路程为．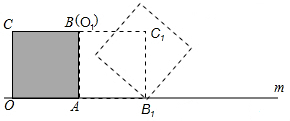

如图，△ABC中，，，，D是线段BC上的一个动点（包括点B,C），以AD为直径画⊙O分别交AB，AC于点E，F，连接EF，则过点E，D，F三点的弓形的面积S的取值范围是__________．

如图，在平面直角坐标系中，⊙O的半径为2，AC、BD是⊙O的两条相互垂直的弦，垂足为M（1，），则四边形ABCD的面积的最大值与最小值的差为______.

如图，△OAB中，OA=OB=4，∠A=30°，AB与⊙O相切于点C，则图中阴影部分的面积为
.（结果保留π）

如图，在矩形ABCD中，AB=2，BC=4，⊙D的半径为1．现将一个直角三角板的直角顶点与矩形的对称中心O重合，绕着O点转动三角板，使它的一条直角边与⊙D切于点H，此时两直角边与AD交于E，F两点，则EH的值为 ．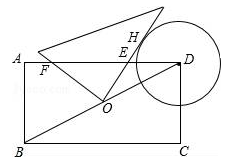

如图，在正方形网格图中建立一直角坐标系，一条圆弧经过网格点A、B、C，请在网格图中进行下列操作：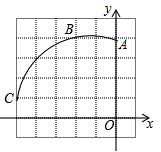

（1）利用网格确定该圆弧所在圆的圆心D点的位置，并写出点D坐标为 ；
（2）连接AD、CD，则⊙D的半径为 （结果保留根号），∠ADC的度数为 ；
（3）若扇形DAC是一个圆锥的侧面展开图，则该圆锥底面半径为 ．（结果保留根号）．

已知△ABC内接于⊙O，过点A作直线EF．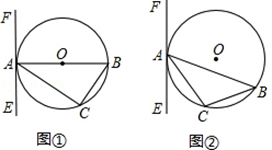

（1）如图①所示，若AB为⊙O的直径，要使EF成为⊙O的切线，还需要添加的一个条件是（至少说出两种）： 或者 ．
（2）如图②所示，如果AB是不过圆心O的弦，且∠CAE=∠B，那么EF是⊙O的切线吗？试证明你的判断．

如图，抛物线y=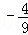x²通过平移得到抛物线m，抛物线m经过点B（6，0）和O（0，0），它的顶点为A，以O为圆心，OA为半径作圆，在第四象限内与抛物线y=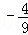x²交于点C，连接AC，则图中阴影部分的面积为　

如图，已知点A（0，1），B（0，-1），以点A为圆心，AB为半径作圆，交x轴的正半轴于点C，则∠BAC等于 度．

如图，P是双曲线（x＞0）的一个分支上的一点，以点P为圆心，1个单位长度为半径作⊙P，当⊙P与直线y＝3相切时，点P的坐标为．

如图，已知△ABC，外心为O，BC=6，∠BAC=60°，分别以AB、AC为腰向形外作等腰直角三角形△ABD与△ACE，连接BE、CD交于点P，则OP的最小值是_________．