如图，将一把两边都带有刻度的直尺放在半圆形纸片上，使其一边经过圆心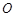
，另一边所在直线与半圆相交于点
，量出半径
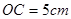，弦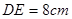
，求这把直尺的宽度．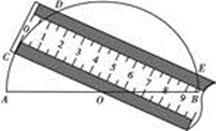
如图所示，
是⊙O的一条弦，
，垂足为
，交⊙O于点
，点
在⊙O
上．
（1）若
，求
的度数；
（2）若
，
，求的长．
已知：如图△ABC中，AC=BC，以BC为直径的⊙O交AB于点D，过点D作DE⊥AC于E，交BC的延长线于点F．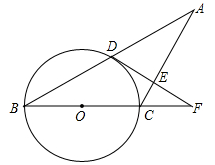
求证：（1）AD=BD；
（2）DF是⊙O的切线．
如图，已知等边
，以边BC为直径的半圆与边AB,AC分别交于点D、E,过点D作DF⊥AC于点F，
（1）判断DF与⊙O的位置关系，并证明你的结论；
（2）过点F作FH⊥BC于点H，若等边的边长为8，求AF，FH的长。
如图，△ABC中，以AB为直径的⊙O交AC于点D，∠DBC=∠BAC．
（1）求证：BC是⊙O的切线．
（2）若⊙O的半径为2，∠BAC=30°，求图中阴影部分的面积．
已知：如图，AB是⊙O的直径，CD是⊙O的弦，且AB⊥CD，垂足为E，连接OC，OC=5．
（1）若CD=8，求BE的长；
（2）若∠AOC=150°，求扇形OAC的面积
如图，AB是⊙O的直径，C是半圆O上的一点，AC平分∠DAB，AD⊥CD，垂足为D，AD交⊙O于E，连接CE．
（1）判断CD与⊙O的位置关系，并证明你的结论；
（2）若E是
的中点，⊙O的半径为1，求图中阴影部分的面积．
如图，边长为4的等边△AOB的顶点O在坐标原点，点A在x轴正半轴上，点B在第一象限．一动点P沿x轴以每秒1个单位长度的速度由点O向点A匀速运动，当点P到达点A时停止运动，设点P运动的时间是t秒．在点P的运动过程中，线段BP的中点为点E，将线段PE绕点P按顺时针方向旋转60º得PC．
（1）当点P运动到线段OA的中点时， 点C的坐标为 ；
（2）在点P从点O到点A的运动过程中，用含t的代数式表示点C的坐标；
（3）在点P从点O到点A的运动过程中，求出点C所经过的路径长．
如图，在直角坐标系中，⊙P的圆心P在x轴上，⊙P与x轴交于点E、F，与y轴交于点C、D，且EO=1，CD=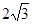
，又B、A两点的坐标分别为（0，m）、（5，0）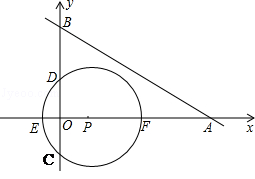
（1）当m=3时，求经过A、B两点的直线解析式；
（2）当B点在y轴上运动时，若直线AB与⊙P保持相交，求m的取值范围．
如图，在△ABC中，AB=AC，以AB为直径的⊙O交AC与E，交BC与D．
求证：
（1）D是BC的中点；
（2）△BEC∽△ADC；
（3）若
，求⊙O的半径。
已知，如图，在Rt△ABC中，∠C=90°，∠BAC的角平分线AD交BC边于D．
（1）以AB边上一点O为圆心，过A，D两点作⊙O（不写作法，保留作图痕迹），再判断直线BC与⊙O的位置关系，并说明理由；
（2）若（1）中的⊙O与AB边的另一个交点为E，AB=6，BD=
，求⊙O的半径．
如图在Rt△ABC中，∠C＝90°，点D是AC的中点，且∠A＋∠CDB＝90°，过点A、D作⊙O，使圆心O在AB上，⊙O与AB交于点E．
（1）求证：直线BD与⊙O相切；
（2）若AD：AE＝4：5，BC＝6，求⊙O的直径．
如图，在平面直角坐标系xOy中，⊙A与y轴相切于点B（0，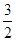
），与x轴相交于M，N两点，如果点M的坐标为（
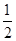，0），求点N的坐标
粤公网安备 44130202000953号