初中数学圆幂定理解答题

如图，在△ABC中，AB=AC，D是BC中点，AE平分∠BAD交BC于点E，点O是AB上一点，⊙O过A、E两点，交AD于点G，交AB于点F．

（1）求证：BC与⊙O相切；
（2）当∠BAC=120°时，求∠EFG的度数．

已知：如图，P是⊙O直径AB延长线上一点，过P的直线交⊙O于C、D两点，弦DF⊥AB于点H，CF交AB于点E。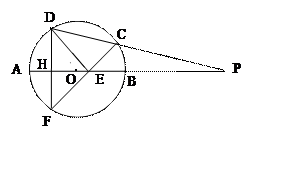

⑴ 求证：PC·PD=PO·PE；
⑵ 若DE⊥CF，∠P=15⁰，⊙O的半径为2，求弦CF的长

如图，方格纸中每个小正方形的边长均为1，△ABC的顶点均在小正方形的顶点处．

（1）以点A为旋转中心，把△ABC顺时针旋转90°，画出旋转后的△；
（2）在（1）的条件下，求点C运动到点所经过的路径长．

如图，在Rt△ABC中，∠ACB=90°，以AC为直径作⊙O交AB于点D，连接CD．

（1）求证：∠A=∠BCD；
（2）若M为线段BC上一点，试问当点M在什么位置时，直线DM与⊙O相切？并说明理由．

如图，在直角坐标系中，⊙P的圆心P在x轴上，⊙P与x轴交于点E、F，与y轴交于点C、D，且EO=1，CD=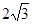，又B、A两点的坐标分别为（0，m）、（5，0）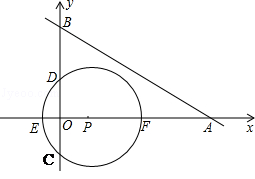

（1）当m=3时，求经过A、B两点的直线解析式；
（2）当B点在y轴上运动时，若直线AB与⊙P保持相交，求m的取值范围．

如图，在△ABC中，AB=AC，以AB为直径的⊙O交AC与E，交BC与D．

求证：
（1）D是BC的中点；
（2）△BEC∽△ADC；
（3）若，求⊙O的半径。

已知，如图，在Rt△ABC中，∠C=90°，∠BAC的角平分线AD交BC边于D．

（1）以AB边上一点O为圆心，过A，D两点作⊙O（不写作法，保留作图痕迹），再判断直线BC与⊙O的位置关系，并说明理由；
（2）若（1）中的⊙O与AB边的另一个交点为E，AB=6，BD=，求⊙O的半径．

如图在Rt△ABC中，∠C＝90°，点D是AC的中点，且∠A＋∠CDB＝90°，过点A、D作⊙O，使圆心O在AB上，⊙O与AB交于点E．

（1）求证：直线BD与⊙O相切；
（2）若AD：AE＝4：5，BC＝6，求⊙O的直径．

如图，在平面直角坐标系xOy中，⊙A与y轴相切于点B（0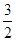，），与x轴相交于M，N两点，如果点M的坐标为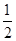（，0），求点N的坐标

如图，四边形ABCD内接于⊙O，BC是直径，∠BAD=120°，AB=AD．

（1）求证：四边形ABCD是等腰梯形；
（2）已知AC=6，求阴影部分的面积．

如图，⊙O的直径AB为10cm，弦BC为5cm，D、E分别是∠ACB的平分线与⊙O，AB的交点，P为AB延长线上一点，且PC=PE．

（1）求AC、AD的长；
（2）试判断直线PC与⊙O的位置关系，并说明理由．

如图，AB 是半圆O 的直径，AD 和BC 是它的两条切线，切点分别为A、B，CO 平分∠BCD．

（1）求证：CD是半圆O的切线；
（2）若AC=2，BD=3，求AB的长．．

图1为一锐角是30°的直角三角尺，其边框为透明塑料制成（内、外直角三角形对应边互相平行且三处所示宽度相等）．
操作：将三角尺移向直径为4cm的⊙O，它的内Rt△ABC的斜边AB恰好等于⊙O的直径，它的外Rt△A′B′C′的直角边A′C′ 恰好与⊙O相切（如图2）．
思考：

（1）求直角三角尺边框的宽；
（2）求BB′C′+CC′B′的度数；
（3）求边B′C′的长．

已知：如图，矩形ABCD中，CD＝2，AD＝3，以C点为圆心，作一个动圆，与线段AD交于点P（P和A、D不重合），过P作⊙C的切线交线段AB于F点.

（1）求证：△CDP∽△PAF；
（2）设，，求关于的函数关系式，及自变量的取值范围；
（3）是否存在这样的点P，使△APF沿PF翻折后，点A落在BC上，请说明理由.

某中学在校内安放了几个圆柱形饮水桶的木制支架（如图①），若不计木条的厚度，其俯视图如图②所示，已知AD垂直平分BC，AD＝BC＝40cm，则圆柱形饮水桶的底面半径的最大值是____▲ _____cm.