已知：如图，矩形ABCD中，CD＝2，AD＝3，以C点为圆心，作一个动圆，与线段AD交于点P（P和A、D不重合），过P作⊙C的切线交线段AB于F点.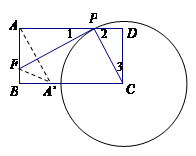
（1）求证：△CDP∽△PAF；
（2）设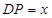
，
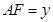，求
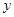关于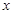
的函数关系式，及自变量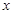的取值范围；
（3）是否存在这样的点P，使△APF沿PF翻折后，点A落在BC上，请说明理由.
的两根的绝对值相等，求
的值及这个方程的根。
的两根，求矩形的周长和面积。
有两个正实根，求k的取值范围.
的两实根的绝对值相等，求出与k值相应的实数根.
是关于x的方程
的两个实根，k取什么值时，
.推荐套卷
已知：如图，矩形ABCD中，CD＝2，AD＝3，以C点为圆心，作一个动圆，与线段AD交于点P（P和A、D不重合），过P作⊙C的切线交线段AB于F点.
（1）求证：△CDP∽△PAF；
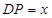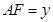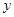（2）设，，求关于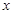的函数关系式，及自变量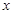的取值范围；
（3）是否存在这样的点P，使△APF沿PF翻折后，点A落在BC上，请说明理由.
粤公网安备 44130202000953号