如图四边形ABCD中,已知∠A=∠C=30°,∠D=60°,AD=8,CD=10.
(1)求AB、BC的长;
(2)已知,半径为1的⊙P在四边形ABCD的外面沿各边滚动(无滑动)一周,求⊙P在整个滚动过程中所覆盖部分图形的面积.
一张圆心角为45°的扇形纸板和圆形纸板按如图方式分别剪成一个正方形,边长都为1,则扇形和圆形纸板的面积比是 ( )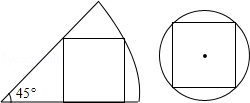
| A.5:4 | B.5:2 | C.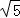 :2 :2 |
D.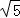 : :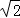 |
(本小题满分10分)
有一学校为了解九年级学生某次体育测试成绩,现对这次体育测试成绩进行抽样调查,结果统计如下,其中扇形统计图中E组所在的扇形的圆心角为144°
被抽取的体育测试成绩频数分布表
| 组别 |
成绩 |
频数 |
| A |
20<x≤24 |
2 |
| B |
24<x≤28 |
3 |
| C |
28<x≤32 |
5 |
| D |
32<x≤36 |
b |
| E |
36<x≤40 |
20 |
| 合计 |
a |

根据上面的图表提供的信息,回答下列问题:
(1)计算频数分布表中a与b的值;
(2)请估计该校九年级学生这次体育测试成绩的平均分(结果取整数)
(3)小敏测得扇形统计图的半径为5,将扇形统计图的A,B,C区域块剪下来,剩余部分卷成圆锥体(不算重合部分),则圆锥体的高为多少?
如图,AB是⊙O的直径,点F,C是⊙O上两点,且 ,连接AC,AF,过点C作CD⊥AF交AF延长线于点D,垂足为D.
,连接AC,AF,过点C作CD⊥AF交AF延长线于点D,垂足为D.
(1)求证:CD是⊙O的切线;
(2)若CD=2 ,求⊙O的半径.
,求⊙O的半径.
如图,AB为半圆O的直径,点C在半圆上,CD⊥AB于点D,连结BC,作∠BCP=∠BCD,CP交AB延长线于点P.
(1)求证:PC是半圆O的切线;
(2)求证:PC2=PB•PA;
(3)若PC=2,tan∠BCD= ,求
,求 的长.
的长.
如图所示,AB是⊙O的弦,D为OA半径的中点,过D作CD⊥OA交弦AB于点E,交⊙O于点F,且CE=CB.
(1)求证:BC是⊙O的切线;
(2)连接AF,BF,求∠ABF的度数;
(3)如果CD=15,BE=10,sinA= ,求⊙O的半径
,求⊙O的半径
如图,已知AB是⊙O的直径,AB=8, 点C在半径OA上(点C与点O、A不重合),过点C作AB的垂线交⊙O于点D,连结OD,过点B作OD的平行线交⊙O于点E、交射线CD于点F.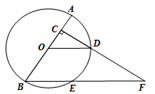
(1)若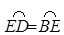 ,求∠F的度数;
,求∠F的度数;
(2)设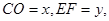 写出
写出 与
与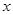 之间的函数解析式,并写出自变量取值范围;
之间的函数解析式,并写出自变量取值范围;
(3)设点C关于直线OD的对称点为P,若△PBE为等腰三角形,求OC的长.
在△ABC中,∠A=90°,AB=8,AC=6,M是AB上的动点(不与A,B重合),过M点作MN∥BC交AC于点N.以MN为直径作⊙O,并在⊙O内作内接矩形AMPN.设AM= .
. 

(1)用含 的代数式表示△MNP的面积S;
的代数式表示△MNP的面积S;
(2)在动点M的运动过程中,记△MNP与梯形BCNM重合部分的面积为 ,试求
,试求 关于
关于 的函数表达式,并求
的函数表达式,并求 为何值时,
为何值时, 的值最大,最大值是多少?
的值最大,最大值是多少?
(1)如图1,△ACB和△DCE均为等边三角形,点A,D,E在同一直线上,连接BE.①∠AEB的度数为 ;② 线段AD,BE之间的数量关系为 ;
(2)如图2,△ACB和△DCE均为等腰直角三角形,∠ACB=∠DCE=90°,点A,D,E在同一直线上,CM为△DCE中DE边上的高,连接BE,请判断∠AEB的度数及线段CM,AE,BE之间的数量关系,并说明理由;
(3)如图3,在正方形ABCD中,CD= ,若点P满足PD=1,且∠BPD=90°,请直接写出点A到BP的距离.
,若点P满足PD=1,且∠BPD=90°,请直接写出点A到BP的距离.
如图,在RtΔABC中,∠C=90°,AC=3,BC=4,P为边AC上一个点(可以包括点C但不包括点A),以P为圆心PA为半径作⊙P交AB于点D,过点D作OP的切线交边BC于点E.试猜想BE与DE的数量关系,并说明理由.
如图,AB是⊙O的直径,OD垂直于弦AC于点E,且交⊙O于点D,F是BA延长线上一点,若∠CDB=BFD.
(1)求证:FD是⊙O的一条切线;
(2)若AB=10,AC=8,求DF的长.
如图,△ABC中,∠ABC=900,以AB为直径的⊙O交AC于D.E为弧AD上一点,连结AE,BE,BE交AC于点F,且

(1)求证:E是弧AD的中点。
(2)求证:CB=CF
(3)若点E到弦AD的距离为1, ,求⊙O的半径。
,求⊙O的半径。
如图,在Rt△ABC中,∠BCA=900,∠BAC的平分线交△ABC外接圆于点D,连接BD,若AB=2AC=4。(1)则BD长为_______。(2)设点P在优弧CAB上由点C向点B移动,但不与点C、B重合,记∠PBC的角平分线与PD交点为I,点I随点P的移动所经过的路径长l的取值范围是_________________。