北京市八一学校九年级零模数学试卷
节约是一种美德,节约是一种智慧.据不完全统计,全国每年浪费食物总量折合粮食可养活约3亿5千万人.350 000 000用科学记数法表示为
| A.3.5×107 | B.3.5×108 | C.3.5×109 | D.3.5×1010 |
某次考试后,班里有两位同学议论他们所在小组同学的数学成绩,小明说:“我们组成绩是86分的同学最多”,小英说:“我们组的7位同学成绩排在最中间的恰好也是86分”,上面两位同学的话能反映出的统计量是
| A.众数和平均数 | B.平均数和中位数 |
| C.众数和方差 | D.众数和中位数 |
如图,有以下3个条件:①AC=AB,②AB∥CD,③∠1=∠2,从这3个条件中任选2个作为题设,另1个作为结论,则组成的命题是真命题的概率是 
| A.0 | B. |
C. |
D.1 |
点P从点O出发,按逆时针方向沿周长为l的图形运动一周,O,P两点间的距离y与点P走过的路程x的函数关系如图,那么点P所走的图形是 

如图,某人将一块正五边形玻璃打碎成四块,现要到玻璃店配一块完全一样的玻璃,那么最省事的方法是带_____________块.
如图,将矩形ABCD沿AE折叠,点D恰好落在BC边上的点F处,若AB:AD=2:3,则tan∠AFB值是 .
如图,OB是⊙O的半径,弦AB=OB,直径CD⊥AB.若点P是线段OD上的动点,连接PA,则∠PAB的度数可以是 (写出一个即可)
已知:如图,C为BE上一点, 点A、D分别在BE两侧,AB∥ED,∠ACB=∠CDE,BC=ED.求证:AC=CD.
已知一次函数
 与反比例函数
与反比例函数 的图象交于A(2,3), B(-6,n) 两点.
的图象交于A(2,3), B(-6,n) 两点.
(1)求一次函数和反比例函数的解析式;
(2)P是y轴上一点,且 ,直接写出P点坐标.
,直接写出P点坐标.
列方程或方程组解应用题:
某工程队改造一条长2 500米的道路.在改造了1 000米后,为了减少施工对交通造成的影响,采用了新的施工工艺,使每天的工作效率是原来的1.5倍,结果提前5天完成任务.求原来每天改造道路多少米?
如图,在平行四边形ABCD中,E,F分别为边AB,CD的中点,BD是对角线,过A点作AG∥DB交CB的延长线于点G .
(1)求证:四边形DEBF是平行四边形;
(2)如果 ∠G=90°, ∠C=60°, BC=2, 求四边形DEBF的面积.
从2015年1月7日起,中国中东部大部分地区持续出现雾霾天气。某市记者为了了解“雾霾天气的主要成因”,随机调查了该市部分市民,并对调查结果进行整理,绘制了如下尚不完整的统计图表.
请根据图表中提供的信息解答下列问题:
(1) 填空:m= ,n= ,扇形统计图中E组所占的百分比为 %.
(2) 若该市人口约有100万人,请你计算其中持D组“观点”的市民人数.
(3) 若在这次接受调查的市民中,随机抽查一人,则此人持C组“观点”的概率是多少?
如图,AB是⊙O的直径,点C在⊙O上,CE^ AB于E, CD平分ÐECB, 交过点B的射线于D, 交AB于F, 且BC=BD.

(1)求证:BD是⊙O的切线;
(2)若AE=9, CE=12, 求BF的长.
已知,如图,直线AB与直线BC相交于点B,点D是直线BC上一点.求作:点E,使直线DE∥AB,且点E到B、D两点的距离相等.(在题目的原图中用尺规完成作图, 并且保留作图痕迹)
结论:
已知二次函数y=(t-4)x2-(2t-5)x+4在x=0与x=5的函数值相等.
(1)求二次函数的解析式;
(2)若二次函数的图象与x轴交于A,B两点(A在B左侧),与y轴交于点C,一次函数y=kx+b经过B,C两点,求一次函数的表达式;
(3)在(2)的条件下,过动点D(0,m) 作直线 //x轴,其中
//x轴,其中 .将二次函数图象在直线
.将二次函数图象在直线 下方的部分沿直线
下方的部分沿直线 向上翻折,其余部分保持不变,得到一个新图象M.若直线
向上翻折,其余部分保持不变,得到一个新图象M.若直线 与新图象M恰有两个公共点,请求出
与新图象M恰有两个公共点,请求出 的取值范围.
的取值范围.
(1)如图1,△ACB和△DCE均为等边三角形,点A,D,E在同一直线上,连接BE.①∠AEB的度数为 ;② 线段AD,BE之间的数量关系为 ;
(2)如图2,△ACB和△DCE均为等腰直角三角形,∠ACB=∠DCE=90°,点A,D,E在同一直线上,CM为△DCE中DE边上的高,连接BE,请判断∠AEB的度数及线段CM,AE,BE之间的数量关系,并说明理由;
(3)如图3,在正方形ABCD中,CD= ,若点P满足PD=1,且∠BPD=90°,请直接写出点A到BP的距离.
,若点P满足PD=1,且∠BPD=90°,请直接写出点A到BP的距离.
如图①,直线l:y=mx+n(m<0,n>0)与x,y轴分别相交于A,B两点,将△AOB绕点O逆时针旋转90°,得到△COD,过点A,B,D的抛物线P叫做l的关联抛物线,而l叫做P的关联直线.
(1)若l:y=﹣2x+2,则P表示的函数解析式为 ;若P:y=﹣x2﹣3x+4,则l表示的函数解析式为 .
(2)求P的对称轴(用含m,n的代数式表示);
(3)如图②,若l:y=﹣2x+4,P的对称轴与CD相交于点E,点F在l上,点Q在P的对称轴上.当以点C,E,Q,F为顶点的四边形是以CE为一边的平行四边形时,求点Q的坐标;
(4)如图③,若l:y=mx﹣4m,G为AB中点,H为CD中点,连接GH,M为GH中点,连接OM.若OM= ,直接写出l,P表示的函数解析式.
,直接写出l,P表示的函数解析式.
 的相反数是
的相反数是









 中,自变量
中,自变量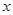 的取值范围是 .
的取值范围是 .

 的整数解.
的整数解. ,求代数式
,求代数式 的值.
的值. 粤公网安备 44130202000953号
粤公网安备 44130202000953号