如图，AB是⊙O的直径，点C在⊙O上，CE^ AB于E， CD平分ÐECB， 交过点B的射线于D， 交AB于F， 且BC=BD．
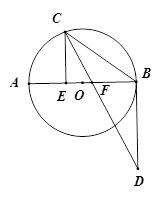
（1）求证：BD是⊙O的切线；
（2）若AE=9， CE=12， 求BF的长．
.
；
.
还少40º，求这个角.
相关知识点
推荐套卷
如图，AB是⊙O的直径，点C在⊙O上，CE^ AB于E， CD平分ÐECB， 交过点B的射线于D， 交AB于F， 且BC=BD．
（1）求证：BD是⊙O的切线；
（2）若AE=9， CE=12， 求BF的长．
粤公网安备 44130202000953号