初中数学三角形的五心解答题

如图所示，已知AC∥BD，EA，EB分别平分∠CAB和∠DBA，CD过E点．求证：AB＝AC＋BD．

已知△中，（如图），点到两边的距离相等，且．
（1）先用尺规作出符合要求的点（保留作图痕迹，不需要写作法），然后判断△的形状，并说明理由；
（2）设，，试用、的代数式表示的周长和面积；
（3）设与交于点，试探索当边、的长度变化时，的值是否发生变化，若不变，试求出这个不变的值，若变化，试说明理由．

（1）如图1，在△ABC中，∠ABC的平分线BF交AC于F，过点F作DF∥BC，求证：BD=DF．
（2）如图2，在△ABC中，∠ABC的平分线BF与∠A CB的平分线CF相交于F，过点F作DE∥BC，交直线AB于点D，交直线AC于点E．那么BD，CE，DE之间存在什么关系 ？并证明这种关系．
（3）如图3，在△ ABC中，∠ABC的平分线BF与∠ACB的外角平分线CF相交于F，过点F作DE∥BC，交直线AB于点D，交直线AC于点E．那么BD，CE，DE之间存在什么关系？请写出你的猜想．（不需证明）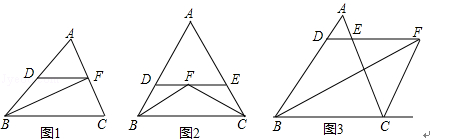

如图，在△ABC和△DEF中，AC∥DE，∠EFD与∠B互补，DE=mAC（m＞1）．试探索线
段EF与AB的数量关系，并证明你的结论．

如图，在矩形纸片ABCD中，AB=4，AD=12，将矩形纸片折叠，使点C落在AD边上的点M处，折痕为PE，此时PD=3．

（1）求MP的值；
（2）在AB边上有一个动点F，且不与点A，B重合．当AF等于多少时，△MEF的周长最小？
（3）若点G，Q是AB边上的两个动点，且不与点A，B重合，GQ=2．当四边形MEQG的周长最小时，求最小周长值．（计算结果保留根号）

如图，直线与轴负半轴、轴正半轴分别交于A、B两点，正比例函数的图像与直线AB交于点Q，过A、B两点分别作AM⊥OQ于M，BN⊥OQ于N，若AM =10，BN =3，
（1）求A、B两点的坐标；（用b表示）
（2）图中有全等的三角形吗？若有，请找出并说明理由。
（3）求MN的长．

已知：如图1，△ABC中，AB＝13，BC＝14，AC＝15．将线段AB沿过点A的直线翻折，使得点B的对应点E恰好落在BC边上，折痕与BC边相交于点D，如图2所示．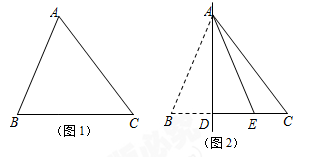

（1） 求线段DE的长；
（2） 在图2中，若点P为线段AC上一点，且△AEP为等腰三角形，求AP的长．
小李在解决第（2）小题时的过程如下：
① 当EA＝EP时，显然不存在；当AE＝AP时，则AP＝__________；（需填空）
② 对于“当PA＝PE时的情形”，小李在解决时遇到了困难．小明老师对小李说：对于这个“直线形”图形直接解决困难时，我们可以建立平面直角坐标系，用一次函数的知识解决．如以点D为坐标原点，BC所在直线为x轴，然后求出AE中垂线的直线解析式，然后求出点P的坐标，最后用勾股定理求出AP的长……
请根据小明老师的提示完成第（2）题中②的求解，你也可以用自己的方法求出AP的长．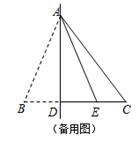

如图，AD⊥BC，垂足为D．CD=1，AD=2，BD=4．

（1）求∠BAC的度数？并说明理由；
（2）P是边BC上一点，连结AP，当△ACP为等腰三角形时，求CP的长．

如图，点A是5×5网格图形中的一个格点，图中每个小正方形的边长为1，请在网格中按下列要求操作：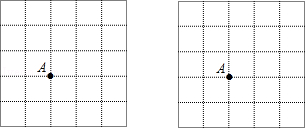

（1）以点A为其中的一个顶点，在图（1）中画一个面积等于3的格点直角三角形；
（2）以点A为其中的一个顶点，在图（2）中画一个面积等于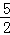的格点等腰直角三角形．

如图，在△ABC中，∠BAC=90°，AB=6cm，BC=10cm，点D在线段AC上，且CD=2cm，动点P从BA的延长线上距A点10cm的E点出发，以每秒2cm的速度沿射线EA的方向运动了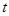秒。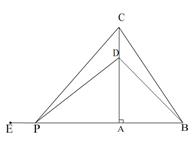

（1）求AD的长；
（2）直接写出用含有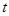的代数式表示PE=_________；
（3）在运动过程中，是否存在某个时刻，使△ABC与△ADP全等？若存在，请求出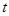值；若不存在，请说明理由．

若一个三角形的三个顶点均在一个图形的不同的边上，则称此三角形为该图形的内接三角形．

（1）在图①中画出△ABC的一个内接直角三角形；
（2）如图②，已知△ABC中，∠BAC＝60°，∠B＝45°，AB＝8，AD为BC边上的高，探究以D为一个顶点作△ABC的内接三角形，其周长是否存在最小值？若存在，请求出最小值；若不存在，请说明理由；
（3）如图③，△ABC为等腰直角三角形，∠C＝90°，AC＝６，试探究：△ABC的内接等腰直角三角形的面积是否存在最小值？若存在，请求出最小值；若不存在，请说明理由．

如图，已知△ABC中，∠B=90°，AB=8cm，BC=6cm。

（1）若P、Q是△ABC边上的两个动点，其中点P从A沿A→B方向运动，速度为每秒1cm，点Q从B沿B→C方向运动，速度为每秒2cm，两点同时出发，设出发时间为t秒．①当t=1秒时，求PQ的长；②从出发几秒钟后，△PQB是等腰三角形？
（2）若M在△ABC边上沿B→A→C方向以每秒3cm的速度运动，则当点M在边CA上运动时，求△BCM成为等腰三角形时M运动的时间．

已知△ABC三边长都是整数且互不相等，它的周长为12，当BC为最大边时，求∠A的度数．

如图，已知AB是⊙O的直径，AB=8， 点C在半径OA上（点C与点O、A不重合），过点C作AB的垂线交⊙O于点D，连结OD，过点B作OD的平行线交⊙O于点E、交射线CD于点F．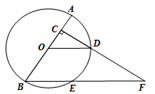

（1）若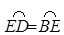，求∠F的度数；
（2）设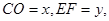写出与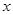之间的函数解析式，并写出自变量取值范围；
（3）设点C关于直线OD的对称点为P，若△PBE为等腰三角形，求OC的长．

在△ABC中，AB=AC，∠BAC=（），将线段BC绕点B逆时针旋转60°得到线段BD。

（1）如图1，直接写出∠ABD的大小（用含的式子表示）；
（2）如图2，∠BCE=150°，∠ABE=60°，判断△ABE的形状并加以证明；
（3）在（2）的条件下，连结DE，若∠DEC=45°，求的值。