已知:如图, ,点
,点 是
是 的中点,
的中点, ,
,  、
、 分别交
分别交 于点
于点 、
、 .
.
(1)图中有几组全等三角形,请把它们直接表示出来;
(2)求证: .
.
如图,在平面直角坐标系中,O为坐标原点.△ABC的边BC在x轴上,A、C两点的坐标分别为A(0,m)、C(n,0),B(﹣5,0),且 ,点P从B出发,以每秒2个单位的速度沿射线BO匀速运动,设点P运动时间为t秒.
,点P从B出发,以每秒2个单位的速度沿射线BO匀速运动,设点P运动时间为t秒.

(1)求A、C两点的坐标;
(2)连接PA,用含t的代数式表示△POA的面积;
(3)当P在线段BO上运动时,是否存在一点P,使△PAC是等腰三角形?若存在,请写出满足条件的所有P点的坐标并求t的值;若不存在,请说明理由.
已知:如图,在 中,
中, °,
°, °
°

(1)作 的平分线
的平分线 ,交
,交 于点
于点 ;作
;作 的中点
的中点
(要求:尺规作图,保留作图痕迹,不必写作法和证明);
(2)连接 ,则
,则 °.
°.
如图,已知:在△AFD和△CEB中,点A、E、F、C在同一直线上,AE=CF, AD=BC,AD∥BC.求证:DF∥BE.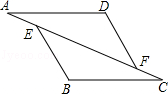
等腰直角△ABC的直角边AB=BC=10cm,点P、Q分别从A,C两点同时出发,均以1cm/s的速度作直线运动,已知P沿射线AB运动,Q沿边BC的延长线运动,PQ与直线AC相交于点D,设P点运动时间为t,△PCQ的面积为S.

(1)求出S关于t的函数关系式;
(2)当P点运动几秒时,S △PCQ=S △ABC?
(3)若P在B的左边时,作PE⊥AC于点E,当点P、Q运动时,线段DE的长度是否改变?证明你的结论.
如图所示,在△ABC中,AC=10,BC=17,CD=8,AD=6.
求:(1)BD的长;
(2)△ABC的面积.
如图所示,在△ABC中,AE、BF是角平分线,它们相交于点O,AD是高,∠BAC=50°,∠C=70°,求∠DAC、∠BOA的度数.
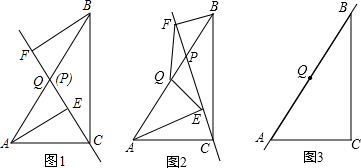
已知,点P是直角三角形ABC斜边AB上一动点(不与A,B重合),分别过A,B向直线CP作垂线,垂足分别为E,F,Q为斜边AB的中点.
(1)如图1,当点P与点Q重合时,AE与BF的位置关系是 ,QE与QF的数量关系式 ;
(2)如图2,当点P在线段AB上不与点Q重合时,试判断QE与QF的数量关系,并给予证明;
(3)如图3,当点P在线段BA(或AB)的延长线上时,此时(2)中的结论是否成立?请画出图形并给予证明.
按要求尺规作图:(不写作法,保留作图痕迹)
已知:线段a,c和∠α.如图所示.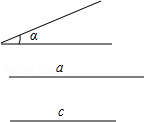
求作:△ABC,使BC=a,AB=c,∠ABC=∠α.
如果三角形有一边上的中线恰好等于这边的长,那么我们称这个三角形为“趣味三角形”.
(1)请用尺规作图的方式,画一个“趣味三角形”(保留作图痕迹);
(2)如图,在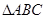 中,∠C=90°,AD是BC边上的中线,已知AC=
中,∠C=90°,AD是BC边上的中线,已知AC=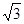 ,BC=2,请判断
,BC=2,请判断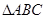 是不是“趣味三角形”,并说明理由。
是不是“趣味三角形”,并说明理由。
如图,在等腰Rt△ABC中,∠ACB=90o,AC=CB,F是AB边上的中点,点D、E分别在AC、BC边上运动,且始终保持AD=CE,连接DE、DF、EF.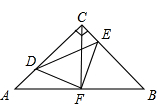
(1)求证:△ADF≌△CEF;
(2)试证明△DFE是等腰直角三角形.
如图,已知△ABC,用直尺(没有刻度)和圆规在平面上求作一个点P,使P到∠A两边的距离相等,且PA=PB.(不要求写作法,但要保留作图痕迹)