等腰直角△ABC的直角边AB=BC=10cm，点P、Q分别从A，C两点同时出发，均以1cm/s的速度作直线运动，已知P沿射线AB运动，Q沿边BC的延长线运动，PQ与直线AC相交于点D，设P点运动时间为t，△PCQ的面积为S．
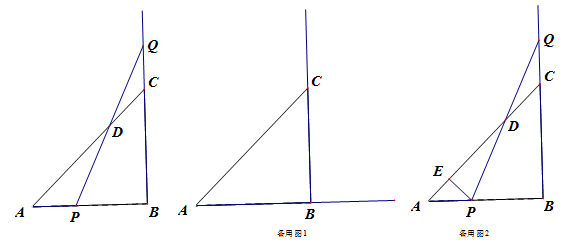
（1）求出S关于t的函数关系式；
（2）当P点运动几秒时，S △PCQ=S △ABC？
（3）若P在B的左边时，作PE⊥AC于点E，当点P、Q运动时，线段DE的长度是否改变？证明你的结论．
相关试题
，AB的垂直平分线DE交BC延长线于E，交AC于F，∠A=50°，
，则（1）△BCF的周长为多少？（2）∠E的度数为多少？
相关知识点
推荐套卷
粤公网安备 44130202000953号