如图,在△ABC中,DE∥BC交AB、AC于点D、E,AD=1,BD=2,那么,△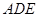 与△
与△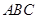 面积的比为( )
面积的比为( )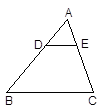
A. 1∶2 B. 1∶3 C. 1∶4 D. 1∶9
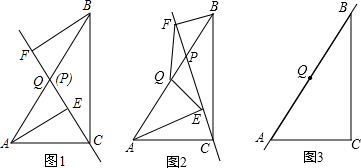
如图1,点P、Q分别是等边△ABC边AB、BC上的动点(端点除外),点P从顶点A、点Q从顶点B同时出发,且它们的运动速度相同,连接AQ、CP交于点M.
(1)求证:△ABQ≌△CAP;
(2)当点P、Q分别在AB、BC边上运动时,∠QMC变化吗?若变化,请说明理由;若不变,求出它的度数.
(3)如图2,若点P、Q在运动到终点后继续在射线AB、BC上运动,直线AQ、CP交点为M,则∠QMC变化吗?若变化,请说明理由;若不变,则求出它的度数.
等边三角形的边长为2,则该三角形的面积为( )
A. |
B. |
C. |
D.3 |
已知,点P是直角三角形ABC斜边AB上一动点(不与A,B重合),分别过A,B向直线CP作垂线,垂足分别为E,F,Q为斜边AB的中点.
(1)如图1,当点P与点Q重合时,AE与BF的位置关系是 ,QE与QF的数量关系式 ;
(2)如图2,当点P在线段AB上不与点Q重合时,试判断QE与QF的数量关系,并给予证明;
(3)如图3,当点P在线段BA(或AB)的延长线上时,此时(2)中的结论是否成立?请画出图形并给予证明.
下列各组数据分别是三角形的三边长,其中不能构成直角三角形的是( )
A.2cm,4cm, cm cm |
B.1cm,1cm,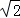 cm cm |
C.1cm,2cm,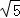 cm cm |
D.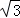 cm,2cm, cm,2cm,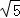 cm cm |
已知三角形的三边长分别是4,6,x.若x的值为奇数,则x的取值有( )
| A.4个 | B.5个 | C.6个 | D.7个 |
如图,△ABC中,DE是AC的垂直平分线,AE=4cm,△ABD的周长为14cm,则△ABC的周长为 .
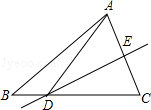
如图,在△ADC中,AD=BD=BC,∠C=30°,则∠ADB=_____.
一个多边形内角和是一个四边形内角和的4倍,则这个多边形的边数是 .
如图,在△ABC中,DE是AC的垂直平分线,AE=3cm,△ABD的周长为13cm,求△ABC的周长.
若△ABC的周长为20cm,点D,E,F分别是△ABC三边的中点,则△DEF的周长为( )
| A.5cm | B.10cm | C.15cm | D. cm cm |
已知在 中,
中, °,
°, °,请画出一条直线,把这个三角形分割成两个等腰三角形(请你选用下面给出的备用图,把所有不同的分割方法都画出来,只需画图,不必说明理由,但要在图中标出相等两角的度数)
°,请画出一条直线,把这个三角形分割成两个等腰三角形(请你选用下面给出的备用图,把所有不同的分割方法都画出来,只需画图,不必说明理由,但要在图中标出相等两角的度数)
在四边形ABCD中,∠ABC+∠ADC=180°,CB=CD.求证:AC平分∠BAD.