初中数学三角形的五心试题

如图4，已知在△ABC和△ADCB中，AC=DB，若不增加任何字母与辅助线，要使△ABC≌△DCB，则还需增加一个条件是_________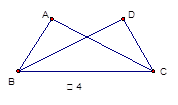

如图2，E是△ABC边BC上的一点，DE垂直平分AB，△ACE的周长是8.5，AB=3，则△ABC的周长为

A．8.5

B．10

C．11.5

D．13

某厂房屋顶呈人字架形（等腰三角形），如图8所示，已知m，，于点

（1）求的大小.
（2）求的长度.

如图2所示，在Rt中，，平分，交于点D，且，则点到的距离是：

A．3

B．4

C．5

D．6

如图，在△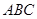中, .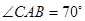

在同一平面内, 将△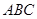绕点A旋转到△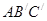的位置, 使得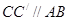, 则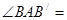

A．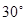

B．

C．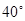

D．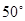

如图，在△ABC中，D、E两点分别在BC、AC边上．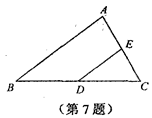

若BD=CD，∠B=∠CDE，DE=2，则AB的长度是
A．4 B．5C．6 D．7

（本小题满分10分）
在图15-1至图15-3中，直线MN与线段AB相交于点O，∠1=∠2=45°．

（1）如图15-1，若AO=OB，请写出AO与BD 的数量关系和位置关系；
（2）将图15-1中的MN绕点O顺时针旋转得到图15-2，其中AO=OB．
求证：AC=BD，AC⊥BD；
（3）将图15-2中的OB拉长为AO的k倍得到图15-3，求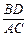的值．

本题满分8分）如图，

已知AD是△ABC的角平分线，在不添加任何辅助线的前提下，要使△AED≌△AFD，需添加一个条件是：_______________，并给予证明.

如图，在△ABC中，

点E、F分别为AB、AC的中点．若EF的长为2，则BC的长为___________.

如图，

把一块直角三角板的直角顶点放在直尺的一边上，如果∠1=35°，那么∠2是_______°．

如图所示，如果将矩形纸沿虚线①对折后，沿虚线②剪开，剪出一个
直角三角形，展开后得到一个等腰三角形.则展开后三角形的周长是（）.

A．2＋

B．2＋2

C．12

D．18

如图5，在Rt△ABC中，∠ACB＝90°，∠BAC＝60°，AB＝6，RtAB′C′可以看作是由Rt△ABC绕点A逆时针方向旋转60°得到的，则线段C′C的长为　 　　　　．

如图10-1，在△A B B′和△A C C′中，∠B A B′=∠C A C′=m°，AC=AC'，AB=AB'．
（1）不添加辅助线的前提下，请写出图中满足旋转变换的两个三角形分别是：；旋转角度是°；
（2）线段BC、B'C'的数量关系是：；试求出BC、B'C'所在直线的夹角：；

（3）随着△ACC'绕点A的旋转，（2）的结论是否依然成立？请从图10-2、图10-3中任选一个证明你的结论；
（4）利用解决上述问题所获得的经验探索下面的问题：如图10-4，等边△ABC外一点D，且∠BDC=60°,连接AD，试探索线段AD、CD、BD的数量关系．

如图，点0是等边△ABC内一点，∠AOB=110°，∠BOC=α，OC=CD,
且∠DOC=60°连接OD.
（1）求证：△COD是等边三角形
（2）当α=150°时，试判断△AOD的形状，并说明理由
（3）探究：当α为多少度时，△AOD是等腰三角形

下列四组线段中（单位cm），能组成三角形的是（　　）

A．2，3，4

B．3，4，7

C．4，6，2

D．7，10，2