初中数学一次函数的最值解答题

某家电生产企业根据市场调查分析，决定调整产品生产方案，准备每周（按120个工时计算）生产空调器、彩电、冰箱共360台，且冰箱至少生产60台，已知生产这些家电产品每台所需工时和每台产值如下表：

家电名称	空调	彩电	冰箱
工 时	1 2	1 3	1 4
产值（千元）	4	3	2

 
问每周应生产空调器、彩电、冰箱各多少台，才能使产值最高？最高产值是多少？（以千元为单位）

开学初，小明到文具批发部一次性购买某种笔记本，该文具批发部规定：这种笔记本售价y（元/本）与购买数量x（本）之间的函数关系如图所示．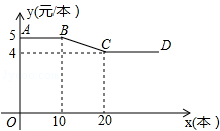

（1）图中线段AB所表示的实际意义是     ；
（2）请直接写出y与x之间的函数关系式；
（3）已知该文具批发部这种笔记本的进价是3元/本，若小明购买此种笔记本超过10本但不超过20本，那么小明购买多少本时，该文具批发部在这次买卖中所获的利润W（元）最大？最大利润是多少？

一个有进水管与出水管的容器，从某时刻开始4min内只进水不出水，在随后的8min内既进水又出水，每分的进水量和出水量有两个常数，容器内的水量y（单位：L）与时间x（单位：min）之间的关系如图所示．

（1）当4≤x≤12时，求y关于x的函数解析式；
（2）直接写出每分进水，出水各多少升．

一农民带上若干千克自产的土豆进城出售，为了方便，他带了一些零钱备用，按市场价售出一些后，又降价出售，售出的土豆千克数与他手中持有的钱数（含备用零钱）的关系，如图所示，结合图象回答下列问题．

（1）农民自带的零钱是多少？
（2）试求降价前y与x之间的关系式？
（3）由表达式你能求出降价前每千克的土豆价格是多少？
（4）降价后他按每千克0．4元将剩余土豆售完，这时他手中的钱（含备用零钱）是26元，试问他一共带了多少千克土豆？

利用图象解方程组．

如图，正方形ABCD、正方形A₁B₁C₁D₁和正方形A₂B₂C₂D₂均位于平面直角坐标系的第一象限内，它们的边平行于x轴或y轴，其中点A，A₁，A₂在直线OM上，点C，C₁，C₂在直线ON上，O为坐标原点，已知点A的坐标为（3，3），正方形ABCD的边长为1．

（1）求直线ON的函数解析式；
（2）若点C₁的横坐标为4，求正方形A₁B₁C₁D₁的边长；
（3）若正方形A₂B₂C₂D₂的边长为m，则点B₂的坐标为                 ．（用含字母m的代数式表示．

一次函数图象经过（3，8）和（5，12）两点，求一次函数解析式．

（本小题满分13分）如图，矩形OABC的顶点A、C分别在x轴和y轴上，点B的坐标为（2，3），双曲线，的图像经过BC上的点D与AB交于点E，连接DE，若若E是AB的中点﹒

（1）求D点的坐标；
（2）点F是OC边上一点，若△FBC和△DEB相似，求BF的解析式；
（3）若点P（m，3m+6）也在此反比例函数的图像上（其中m >0），过p点作x轴的垂线，交x轴于点M，若线段PM上存在一点Q，使得△OQM的面积是，设Q点的纵坐标为n，求的值．

为奖励在演讲比赛中获奖的同学，班主任派学习委员小明为获奖同学买奖品，要求每人一件．小明到文具店看了商品后，决定奖品在钢笔和笔记本中选择．如果买4个笔记本和2支钢笔，则需86元；如果买3个笔记本和1支钢笔，则需57元．
（1）求购买每个笔记本和钢笔分别为多少元？
（2）售货员提示，买钢笔有优惠，具体方法是：如果买钢笔超过10支，那么超出部分可以享受8折优惠，若买x（x＞0）支钢笔需要花y元，请你求出y与x的函数关系式；
（3）在（2）的条件下，小明决定买同一种奖品，数量超过10个，请帮小明判断买哪种奖品省钱．

小锋家有一块四边形形状的空地（如图，四边形ABCD），其中AD∥BC，BC=1.6m，AD=5.5m，CD=5.2m，∠C=90°，∠A=53°．小锋的爸爸想买一辆长4.9m，宽1.9m的汽车停放在这块空地上，让小锋算算是否可行．
小锋设计了两种方案，如图1和图2所示．

（1）请你通过计算说明小锋的两种设计方案是否合理；
（2）请你利用图3再设计一种有别于小锋的可行性方案，并说明理由．
（参考数据：sin53°=0.8，cos53°=0.6，tan53°=）

如图，直线l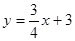：  交x、y轴分别为A、B两点，C点与A点关于y轴对称．动点P、Q分别在线段AC、AB上（点P不与点A、C重合），满足∠BPQ=∠BAO．

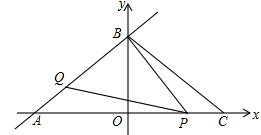
（1）点A坐标是__________，点B的坐标__________，BC=__________．
（2）当点P在什么位置时，△APQ≌△CBP，说明理由．
（3）当△PQB为等腰三角形时，求点P的坐标．

如图，直线l：y=x+6交x、y轴分别为A、B两点，C点与A点关于y轴对称．动点P、Q分别在线段AC、AB上（点P不与点A、C重合），满足∠BPQ=∠BAO．

（1）点A坐标是      ，点B的坐标      ，BC=      ．
（2）当点P在什么位置时，△APQ≌△CBP，说明理由．
（3）当△PQB为等腰三角形时，求点P的坐标．

已知一次函数的图象过点（3，5）与（﹣4，﹣9），且该图象与x轴、y轴分别交于点A、点B，点O为坐标原点，
（1）求这个一次函数的解析式；
（2）求△OAB的面积．

已知y与x+2成正比例，且当x=1时，y=﹣6．
（1）求y与x的函数关系式．
（2）若点（a，2）在此函数图象上，求a的值．

如图1，已知一次函数y=-x+6分别与x、y轴交于A、B两点，过点B的直线BC交x轴负半轴与点C，且OC=OB.

（1）求直线BC的函数表达式；
（2）如图2，若△ABC中，∠ACB的平分线CF与∠BAE的平分线AF相交于点F，求证：∠AFC=∠ABC；
（3）在x轴上是否存在点P，使△ABP为等腰三角形？若存在，请直接写出P点的坐标；若不存在，请说明理由.