如图,正方形ABCD、正方形A1B1C1D1和正方形A2B2C2D2均位于平面直角坐标系的第一象限内,它们的边平行于x轴或y轴,其中点A,A1,A2在直线OM上,点C,C1,C2在直线ON上,O为坐标原点,已知点A的坐标为(3,3),正方形ABCD的边长为1.
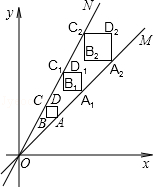
(1)求直线ON的函数解析式;
(2)若点C1的横坐标为4,求正方形A1B1C1D1的边长;
(3)若正方形A2B2C2D2的边长为m,则点B2的坐标为 .(用含字母m的代数式表示.
相关知识点
推荐套卷

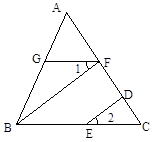
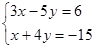 (2)
(2)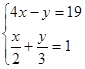
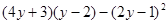 ,y=
,y=
 (2)
(2)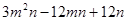 (3)
(3)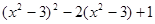
 粤公网安备 44130202000953号
粤公网安备 44130202000953号