初中数学一次函数的最值解答题

对于平面直角坐标系中的任意两点A（a，b），B（c，d），我们把叫做A，B两点之间的直角距离，记作d（A，B）．
（1）已知O为坐标原点，
①若点P坐标为（-1，2），则d（O，P）=____；
②若Q（x，y）在第一象限，且满足d（O，Q）=2，请写出x与y之间满足的关系式，并在平面直角坐标系内画出符合条件的点Q组成的图形．
（2）设M是一定点，N是直线y=mx+n上的动点，我们把d（M，N）的最小值叫做M到直线y=mx+n的直角距离，试求点M（2，-l）到直线y=x+3的直角距离．

先阅读短文，然后回答短文后面所给出的问题：
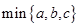对于三个数a、b、c的平均数，最小的数都可以给出符号来表示，我们规定 表示这三个数的平均数，表示这三个数中的最小的数，表示这三个数中最大的数．例如：，，；，．
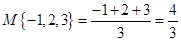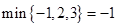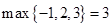（1）请填空：      ；若，则      ；
（2）若，求的取值范围；
（3）若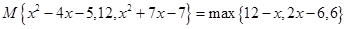，求的值．

（10’）设x_i（i=1，2，3， ，n）为任意代数式，我们规定：y=max{x₁，x₂，x₃，…，x_n}表示x₁，x₂，…，x_n中的最大值，如y=max{1，2}=2．
（1）求y=max{x，3}；
（2）借助函数图象，解决以下问题：
①解不等式 max{x+1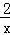，}≥2；
②若函数y=max{|x﹣1|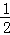，x+a，x²﹣4x+3}的最小值为1，求实数a的值．

某玉米种子的价格为a元/千克，如果一次购买2千克以上的种子，超过2千克部分的种子价格打8折，某科技人员对付款金额和购买量这两个变量的对应关系用列表法做了分析，并绘制出了函数图象，以下是该科技人员绘制的图象和表格的不完全资料，已知点A的坐标为（2，10），请你结合表格和图象：

付款金额（元）	a	7．5	10	12	b
购买量（千克）	1	1．5	2	2．5	3

 
（1）指出付款金额和购买量哪个变量是函数的自变量x，并写出表中a、b的值；
（2）求出当x＞2时，y关于x的函数解析式；
（3）甲农户将88元钱全部用了购买该玉米种子，乙农户购买了4165克该玉米种子，分别计算他们的购买量和付款金额．

在气候对人类生存压力日趋加大的今天，发展低碳经济，全面实现低碳生活成为人们的共识，某企业采用技术革新，节能减排，经分析前5个月二氧化碳排放量y(吨)与月份x(月)之间的函数关系是y=－2x+50．

(1)随着二氧化碳排放量的减少，每排放一吨二氧化碳，企业相应获得的利润也有所提高，且相应获得的利润p(万元)与月份x(月)的函数关系如图所示，那么哪月份，该企业获得的月利润最大？最大月利润是多少万元？
(2)受国家政策的鼓励，该企业决定从6月份起，每月二氧化碳排放量在上一个月的基础上都下降a%，与此同时，每排放一吨二氧化碳，企业相应获得的利润在上一个月的基础上都增加50%，要使今年6、7月份月利润的总和是今年5月份月利润的3倍，求a的值（精确到个位）．
（参考数据： =7.14，=7.21，=7.28，=7.35）

某公司有A型产品40件，B型产品60件，分配给下属甲、乙两个商店销售，其中70件给甲店，30件给乙店，且都能卖完，两商店销售这两种产品每件的利润（元）如下表：

	A型利润	B型利润
甲店	200	170
乙店	160	150

（1）设分配给甲店A型产品x件，这件公司卖出这100件产品的总利润W（元），求W关于x的函数关系式，并求出x的取值范围；
（2）若要求总利润不低于17560元，有多少种不同分配方案，并将各种方案设计出来；
（3）为了促销，公司决定仅对甲店A型产品让利销售，每件让利a元，但让利后A型产品的每件利润仍高于甲店B型产品的每件利润．甲店的B型产品以及乙店的A、B型产品的每件利润不变，问该公司又如何设计分配方案，使总利润达到最大．

（本题共14分）（1）如果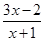=，求m的值；
（2）已知x为整数,且分式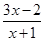的值为整数,则x可取的整数有哪些？
（3）我们知道一次函数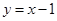的图象可以由函数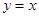的图象向右平移1个单位得到（如图），那么①函数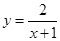的图象可以由函数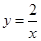经过怎样的平移得到？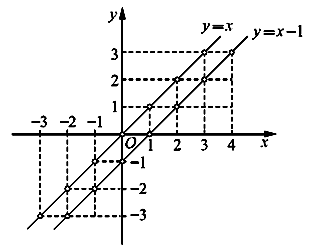

②函数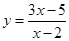的图象可以由函数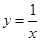经过怎样的平移得到？

如图1，A₁B₁和A₂B₂是水面上相邻的两条赛道（看成两条互相平行的线段）．甲是一名游泳运动健将，乙是一名游泳爱好者，甲在赛道A₁B₁上从A₁处出发，到达B₁后，以同样的速度返回A₁处，然后重复上述过程；乙在赛道A₂B₂上以2m/s的速度从B₂处出发，到达A₂后以相同的速度回到B₂处，然后重复上述过程（不考虑每次折返时的减速和转向时间）．若甲、乙两人同时出发，设离开池边B₁B₂的距离为y（m），运动时间为t（s），甲游动时，y（m）与t（s）的函数图象如图2所示．

（1）赛道的长度是           m，甲的速度是            m/s；
（2）经过多少秒时，甲、乙两人第二次相遇？
（3）若从甲、乙两人同时开始出发到2分钟为止，甲、乙共相遇了       次．2分钟时，乙距池边B₁B₂的距离为多少米．

如图①，已知直线y=3x+3与x轴交于点A，与y轴交于点D，与直线y=交于点E，
过点D作DC∥x轴，交直线y=于点C．过点C作CB∥AD交x轴于点B．
（1）点C的坐标是      ；
（2）以线段AD的中点M为圆心作⊙M，当⊙M与直线CE相切时，求⊙M的半径；
（3）如图②，点P从点O出发，沿线段OC向终点C运动，点Q从点C出发，沿线段CD向终点D运动．若P、Q两点同时出发，速度均为1单位长度/s，时间为ts，当点Q到达终点时，P、Q两点均停止运动．在点P、Q的运动过程中，将线段PQ绕点P沿顺时针方向旋转90°后，设点Q的对应点为R．当点R落在四边形ABCD一边所在的直线上时，直接写出t的值．

一辆慢车与一辆快车分别从甲、乙两地同时出发，匀速相向而行，两车在途中相遇后都停留一段时间，然后分别按原速一同驶往甲地后停车．设慢车行驶的时间为x小时，两车之间的距离为y千米，图中折线表示y与x之间的函数图象，请根据图象解决下列问题：

（1）甲乙两地之间的距离为          千米；
（2）求快车和慢车的速度；
（3）求线段DE所表示的y与x之间的函数关系式，并写出自变量x的取值范围．

如图①，已知直线分别交x轴，y轴于点A，点B．点P是射线AO上的一个动点．把线段PO绕点P逆时针旋转90°得到的对应线段为PO’，再延长PO’ 到C使CO’ = PO’ , 连结AC，设点P坐标为（m，0），△APC 的面积为S．

（1）直接写出OA和OB的长，OA的长是          ， OB的长是          ；
（2）当点P在线段OA上（不含端点）时，求S关于m的函数表达式；
（3）当以A，P，C为顶点的三角形和△AOB相似时，求出所有满足条件的m的值；
（4）如图②，当点P关于OC的对称点P’ 落在直线AB上时，m的值是              ．

如图1，P（2，2），点A在x轴正半轴上运动，点B在y轴上运动，且PA=PB．

（1）求证：PA⊥PB；
（2）若点A（8，0），求点B的坐标；
（3）求OA – OB的值；
（4）如图2，若点B在y轴正半轴上运动时，直接写出OA+OB的值．

甲、乙两人从少年宫出发，沿相同的路分别以不同的速度匀速跑向体育馆，甲先跑一段路程后，乙开始出发，当乙超出甲150米时，乙停在此地等候甲，两人相遇后乙又继续以原来的速度跑向体育馆．如图是甲、乙两人在跑步的全过程中经过的路程y（米）与甲出发的时间x（秒）的函数图象．

（1）在跑步的全过程中，甲共跑了    米，甲的速度为    米/秒；
（2）乙跑步的速度是多少？乙在途中等候甲用了多长时间？
（3）甲出发多长时间第一次与乙相遇？此时乙跑了多少米？

某零件制造车间有工人20名，已知每名工人每天可制造甲种零件6个或乙种零件5个，且每制造一个甲种零件，可获利润150元，每制造一个乙种零件可获利润260元，在这20名工人中，车间每天安排x名工人制造甲种零件，其余工人制造乙种零件，且生产乙种零件的个数不超过甲种零件个数的一半．
（1）请写出此车间每天所获利润y（元）与x（人）之间的函数关系式；
（2）求自变量x的取值范围；
（3）怎样安排生产，每天获得的利润最大，最大利润是多少？

一次函数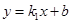的图象经过A（0，﹣2），B（1，0）两点，与反比例函数 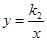的图象在第一象限内的交点为M（m，4）．
（1）求一次函数和反比例函数的表达式；
（2）在x轴上是否存在点P，使AM⊥MP？若存在，求出点P的坐标；若不存在，说明理由．