初中数学一次函数的最值解答题

如图，已知一次函数与反比例函数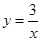的图象交于A，B两点．求A，B两点的坐标．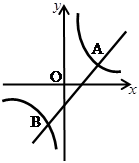

甲、乙两车从A地前往B地，甲车行至AB的中点C处后，以原来速度的1.5倍继续行驶，在整个行程中，汽车离开A地的距离y与时刻t的对应关系如图所示，求：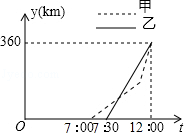

（1）甲车何时到达C地；
（2）甲车离开A地的距离y与时刻t的函数解析式；
（3）乙车出发后何时与甲车相距20km．

某蒜薹（tái）生产基地喜获丰收，收获蒜薹200吨，经市场调查，可采用批发、零售、冷库储藏后销售三种方式，并且按这三种方式销售，计划每吨平均的售价及成本如下表：

销售方式	批发	零售	储藏后销售
售价（百元/吨）	3 0	4 5	5 5
成本（百元/吨）	7	1 0	1 2

 
若蒜薹按计划全部售出获得的总利润为y（百元），蒜薹零售x（吨），且批发量是零售量的3倍．
（1）求y与x之间的函数关系式；
（2）由于受条件限制，经冷库储藏售出的蒜薹最多80吨，求该生产基地按计划全部售完蒜薹获得的最大利润．

我校实行学案教学，需印刷若干份数学学案．印刷厂有甲、乙两种收费方式，除按印数收取印刷费外，甲种方式还需收取制版费而乙种不需要．两种印刷方式的费用y（元）与印刷份数x（份）之间的关系如图所示：

（1）填空：
甲种收费方式的函数关系式是y₁=             ；
乙种收费方式的函数关系式是y₂=             ；
（2）如果我校2014-2015学年八年级每次印刷100～450（含100和450）份学案，选择哪种印刷方式较合算．

在一次蜡烛燃烧试验中，甲、乙两根蜡烛燃烧时剩余部分的高度y（厘米）与燃烧时间x（小时）之间的关系如图所示，请根据图象所提供的信息解答下列问题：

（1）甲、乙两根蜡烛燃烧前的高度分别是          ，从点燃到燃尽甲所用的时间为                  ．
（2）分别求甲、乙两根蜡烛燃烧时y与x之间的函数关系式；
（3）燃烧多长时间时，甲、乙两根蜡烛的高度相等（不考虑都燃尽时的情况）？在什么时间段内，甲蜡烛比乙蜡烛高？在什么时间段内，甲蜡烛比乙蜡低？

在“五•一”期间，“佳佳”网店购进A、B两种品牌的服装进行销售，已知B种品牌服装的进价比A种品牌服装的进价每件高20元，2件A种品牌服装与3件B种品牌服装进价共560元．
（1）求购进A、B两种品牌服 装的单价；
（2）该网站拟以不超过11200元的总价购进这种两品牌服装共100件，并全部售出．其中A种品牌服装的售价为150元/件，B种品牌服装的售价为200元/件，该网站为了获取最大利润，应分别购进A、B两种品牌服装各多少件？所获取的最大利润是多少？

已知，直线m与y的交点在x轴下方，与x轴距离2个单位长度，且直线m过点（1，-1）．
（1）求：直线m的表达式；
（2）求：直线m与x轴的交点坐标；
（3）若直线n与直线m在x轴交于同一点，且直线n与直线m以及y轴所围成的三角形面积为4，请直接写出直线n的表达式．

“五•一”假期，某火车客运站旅客流量不断增大，旅客往往需要长时间排队等候检票．经调查发现，在车站开始检票时，有640人排队检票．检票开始后，仍有旅客继续前来排队检票进站．设旅客按固定的速度增加，检票口检票的速度也是固定的．检票时，每分钟候车室新增排队检票进站16人，每分钟每个检票口检票14人．已知检票的前a分钟只开放了两个检票口．某一天候车室排队等候检票的人数y（人）与检票时间x（分钟）的关系如图所示．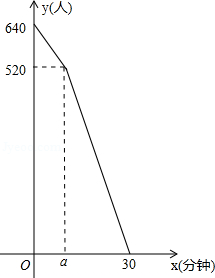

（1）求a的值．
（2）求检票到第20分钟时，候车室排队等候检票的旅客人数．
（3）若要在开始检票后15分钟内让所有排队的旅客都能检票进站，以便后来到站的旅客随到随检，问检票一开始至少需要同时开放几个检票口？

已知一次函数y=kx+b的图象经过点（﹣1，﹣5），且与正比例函数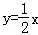的图象相交于点（2，m）．
求：（1）m的值；     
（2）一次函数y=kx+b的解析式；
（3）这两个函数图象与x轴所围成的三角形面积．

“五•一”假期，某火车客运站旅客流量不断增大，旅客往往需要长时间排队等候检票．经调查发现，在车站开始检票时，有640人排队检票．检票开始后，仍有旅客继续前来排队检票进站．设旅客按固定的速度增加，检票口检票的速度也是固定的．检票时，每分钟候车室新增排队检票进站16人，每分钟每个检票口检票14人．已知检票的前a分钟只开放了两个检票口．某一天候车室排队等候检票的人数y（人）与检票时间x（分钟）的关系如图所示．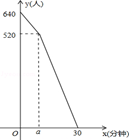

（1）求a的值．
（2）求检票到第20分钟时，候车室排队等候检票的旅客人数．
（3）若要在开始检票后15分钟内让所有排队的旅客都能检票进站，以便后来到站的旅客随到随检，问检票一开始至少需要同时开放几个检票口？

国庆长假，小明从老家乘车去上海．一路上，小明记下了如下数据（注：“上海90km”表示离上海的距离为90km）：

观察时间	10：30（t=0）	10：36（t=6）	10：30（t=18）
路牌内容	上海90Km	上海80Km	上海60Km

 
假设汽车离上海的距离s（km）是行驶时间t（min）的一次函数，求s关于t的函数关系式．

已知一次函数y=kx+b的图象经过点（-1，-5），且与正比例函数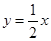的图象相交于点（2，a）．
（1）求a的值．
（2）求一次函数y=kx+b的表达式．
（3）在同一坐标系中，画出这两个函数的图象．

自2012年6月1日起，全国实施了阶梯电价．某省出台了阶梯电价方案：电价分“三档”收费，第一档为a度，居民用电量低于a度的部分，执行现行的标准电价（0．53元/度）；第二档为a～b度，居民月用电量在a～b之间的部分，电价在一档电价的基础上提高0．05元/度；第三档为超过b度，居民月用电量高于b度的部分，电价在一档电价的基础上提高m元/度．实施阶梯电价后，月电费y（元）与月用电量x（度）之间的函数关系如图所示．

（1）求a，b，m的值；
（2）求y与x之间函数关系式，并写出自变量x的取值范围．

某饮料厂为了开发新产品，用种果汁原料和种果汁原料试制新型甲、乙两种饮料共50千克，设甲种饮料需配制千克，两种饮料的成本总额为元．
（1）已知甲种饮料成本每千克4元，乙种饮料成本每千克3元，请你写出与之间的函数关系式．
（2）若用19千克种果汁原料和17．2千克种果汁原料试制甲、乙两种新型饮料，下表是试验的相关数据；

请你列出关于且满足题意的不等式组，求出它的解集，并由此分析如何配制这两种饮料，可使值最小，最小值是多少？

暑假期间，小明和父母一起开车到距家200千米的景点旅游．出发前，汽车油箱内储油45升；当行驶150千米时，发现油箱剩余油量为30升．
（1）已知油箱内余油量y（升）是行驶路程x（千米）的一次函数，求y与x的函数关系式；
（2）当油箱中余油量少于3升时，汽车将自动报警．如果往返途中不加油，他们能否在汽车报警前回到家？请说明理由．