初中数学一次函数的最值解答题

如图，在平面直角坐标系中，过点B（6，0）的直线AB与直线OA相交于点A（4，2），动点M在线段OA和射线AC上运动．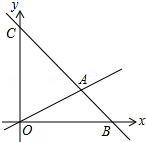

（1）求直线AB的解析式．
（2）求△OAC的面积．
（3）是否存在点M，使△OMC的面积是△OAC的面积的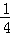？若存在求出此时点M的坐标；若不存在，说明理由．

已知一次函数
（1）若图象交y轴于正半轴，求m的取值范围；
（2）若图象不经过第三象限，求m的取值范围．

如图，请根据图象所提供的信息解答下列问题：

（1）当x   时，kx+b≥mx-n；
（2）不等式kx+b＜0的解集是               ；
（3）交点P的坐标（1，1）是一元二次方程组：           的解；
（4）若直线l₁分别交x轴、y轴于点M、A，直线l₂分别交x轴、y轴于点B、N，求点M的坐标和四边形OMPN的面积．

已知：如图1，一次函数y=mx+5m的图象与x轴、y轴分别交于点A、B，与函数y=-x的图象交于点C，点C的横坐标为-3．
（1）求点B的坐标；
（2）若点Q为直线OC上一点，且S_△QAC=3S_△AOC，求点Q的坐标；
（3）如图2，点D为线段OA上一点，∠ACD=∠AOC．点P为x轴负半轴上一点，且点P到直线CD和直线CO的距离相等．
①在图2中，只利用圆规作图找到点P的位置；（保留作图痕迹，不得在图2中作无关元素．）
②求点P的坐标．

如图，直线y=﹣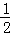x+b交x轴于点A，交直线y=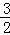x于点B（2，m），矩形CDEF的边DC在x轴上，D在C的左侧，EF在x轴的上方，DC=2，DE=4．当点C的坐标为（﹣2，0）时，矩形CDEF开始以每秒2个单位的速度沿x轴向右运动，运动时间为t秒．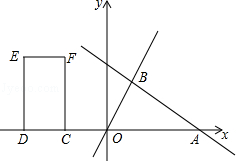

（1）求b，m的值；
（2）矩形CDEF运动t秒时，直接写出C、D两点的坐标（用含t的代数式表示）；
（3）当点B在矩形CDEF的一边上时，求t的值．

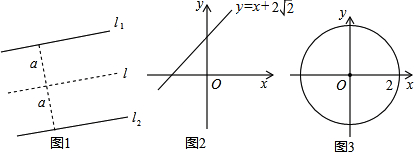
已知到直线l的距离等于a的所有点的集合是与直线l平行且距离为a的两条直线l₁、l₂（如图①）．
（1）在图②的平面直角坐标系中，画出到直线y=x＋2的距离为1的所有点的集合的图形．并写出该图形与y轴交点的坐标．
（2）试探讨在以坐标原点O为圆心，r为半径的圆上，到直线y=x＋2的距离为1的点的个数与r的关系．
（3）如图③，若以坐标原点O为圆心，2为半径的圆上只有两个点到直线y=x＋b的距离为1，则b的取值范围为      ．

“五•一”假期，某火车客运站旅客流量不断增大，旅客往往需要长时间排队等候检票．经调查发现，在车站开始检票时，有640人排队检票．检票开始后，仍有旅客继续前来排队检票进站．设旅客按固定的速度增加，检票口检票的速度也是固定的．检票时，每分钟候车室新增排队检票进站16人，每分钟每个检票口检票14人．已知检票的前a分钟只开放了两个检票口．某一天候车室排队等候检票的人数y（人）与检票时间x（分钟）的关系如图所示．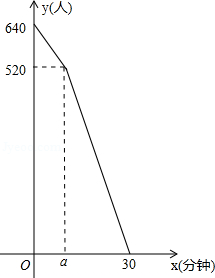

（1）求a的值．
（2）求检票到第20分钟时，候车室排队等候检票的旅客人数．
（3）若要在开始检票后15分钟内让所有排队的旅客都能检票进站，以便后来到站的旅客随到随检，问检票一开始至少需要同时开放几个检票口？

将长为20cm，宽为10cm的长方形白纸，按如图所示的方法粘贴起来，粘合部分的宽为2cm．设x张白纸粘合后的纸条总长度为ycm，

（1）求y与x之间的函数关系式，并画出函数图象，
（2）若x=20，求纸条的面积．

已知一次函数y=kx+b的图象经过点（﹣1，﹣5），且与正比例函数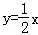的图象相交于点（2，m）．
求：（1）m的值；     
（2）一次函数y=kx+b的解析式；
（3）这两个函数图象与x轴所围成的三角形面积．

“五•一”假期，某火车客运站旅客流量不断增大，旅客往往需要长时间排队等候检票．经调查发现，在车站开始检票时，有640人排队检票．检票开始后，仍有旅客继续前来排队检票进站．设旅客按固定的速度增加，检票口检票的速度也是固定的．检票时，每分钟候车室新增排队检票进站16人，每分钟每个检票口检票14人．已知检票的前a分钟只开放了两个检票口．某一天候车室排队等候检票的人数y（人）与检票时间x（分钟）的关系如图所示．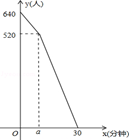

（1）求a的值．
（2）求检票到第20分钟时，候车室排队等候检票的旅客人数．
（3）若要在开始检票后15分钟内让所有排队的旅客都能检票进站，以便后来到站的旅客随到随检，问检票一开始至少需要同时开放几个检票口？

国庆长假，小明从老家乘车去上海．一路上，小明记下了如下数据（注：“上海90km”表示离上海的距离为90km）：

观察时间	10：30（t=0）	10：36（t=6）	10：30（t=18）
路牌内容	上海90Km	上海80Km	上海60Km

 
假设汽车离上海的距离s（km）是行驶时间t（min）的一次函数，求s关于t的函数关系式．

已知一次函数y=kx+b的图象经过点（-1，-5），且与正比例函数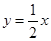的图象相交于点（2，a）．
（1）求a的值．
（2）求一次函数y=kx+b的表达式．
（3）在同一坐标系中，画出这两个函数的图象．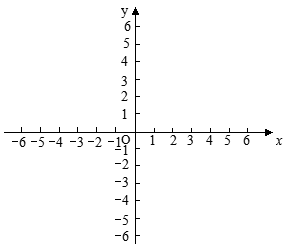

自2012年6月1日起，全国实施了阶梯电价．某省出台了阶梯电价方案：电价分“三档”收费，第一档为a度，居民用电量低于a度的部分，执行现行的标准电价（0．53元/度）；第二档为a～b度，居民月用电量在a～b之间的部分，电价在一档电价的基础上提高0．05元/度；第三档为超过b度，居民月用电量高于b度的部分，电价在一档电价的基础上提高m元/度．实施阶梯电价后，月电费y（元）与月用电量x（度）之间的函数关系如图所示．

（1）求a，b，m的值；
（2）求y与x之间函数关系式，并写出自变量x的取值范围．

某饮料厂为了开发新产品，用种果汁原料和种果汁原料试制新型甲、乙两种饮料共50千克，设甲种饮料需配制千克，两种饮料的成本总额为元．
（1）已知甲种饮料成本每千克4元，乙种饮料成本每千克3元，请你写出与之间的函数关系式．
（2）若用19千克种果汁原料和17．2千克种果汁原料试制甲、乙两种新型饮料，下表是试验的相关数据；

请你列出关于且满足题意的不等式组，求出它的解集，并由此分析如何配制这两种饮料，可使值最小，最小值是多少？

暑假期间，小明和父母一起开车到距家200千米的景点旅游．出发前，汽车油箱内储油45升；当行驶150千米时，发现油箱剩余油量为30升．
（1）已知油箱内余油量y（升）是行驶路程x（千米）的一次函数，求y与x的函数关系式；
（2）当油箱中余油量少于3升时，汽车将自动报警．如果往返途中不加油，他们能否在汽车报警前回到家？请说明理由．