初中数学一次函数的最值解答题

保护生态环境，建设绿色社会已经从理念变为人们的行动．某化工厂2009年1 月的利润为200万元．设2009年1 月为第1个月，第x个月的利润为y万元．由于排污超标，该厂决定从2009年1 月底起适当限产，并投入资金进行治污改造，导致月利润明显下降，从1月到5月，y与x成反比例．到5月底，治污改造工程顺利完工，从这时起，该厂每月的利润比前一个月增加20万元（如图）．

⑴分别求该化工厂治污期间及治污改造工程完工后y与x之间对应的函数关系式．
⑵治污改造工程完工后经过几个月，该厂月利润才能达到2009年1月的水平？
⑶当月利润少于100万元时为该厂资金紧张期，问该厂资金紧张期共有几个月？

我市某工艺品厂生产一款工艺品．已知这款工艺品的生产成本为每件60元．经市场调研发现：该款工艺品每天的销售量y(件)与售价x(元)之间存在着如下表所示的一次函数关系．

售价x(元)	…	70	90	…
销售量y(件)	…	3000	1000	…

（利润＝(售价－成本价)×销售量）
（1）求销售量y(件)与售价x(元)之间的函数关系式；
（2）你认为如何定价才能使工艺品厂每天获得的利润为40 000 元？

红星食品厂独家生产具有地方特色的某种食品，产量y1(万千克)与销售价格x(元／千克)(2≤x≤10)满足函数关系式y1=0.5x+11．经市场调查发现：该食品市场需求量y2(万千克)与销售价格x(元／千克)(2≤x≤10)的关系如图所示．当产量小于或等于市场需求量时，食品将被全部售出；当产量大于市场需求量时，只能售出符合市场需求量的食品，剩余食品由于保质期短将被无条件销毁．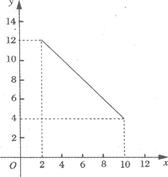

(1)求y2与x的函数关系式；
(2)当销售价格为多少时，产量等于市场需求量?
(3)若该食品每千克的生产成本是2元，试求厂家所得利润W(万元)与销售价格x(元／千克) (2≤x≤10)之间的函数关系式．

我国青海省玉树地区发生强烈地震以后，国家立即启动救灾预案，积极展开灾区运送救灾物资和对伤员的救治工作．已知西宁机场和玉树机场相距800千米，
乙两机沿同一航线各自从西宁、玉树出发，相向而行．如图，线段AB、CD分别表示甲、乙
两机离玉树机场的距离S（百千米）和所用去的时间t（小时）之间的函数关系的图象（注：
为了方便计算，将平面直角坐标系中距离S的单位定为（百千米））．观察图象回答下列问题：
（1）乙机在甲机出发后几小时，才从玉树机场出发？甲、乙两机的飞行速度每小时各为多少千米？
（2）求甲、乙两机各自的S与t的函数关系式；
（3）甲、乙两机相遇时，乙机飞行了几小时？离西宁机场多少千米？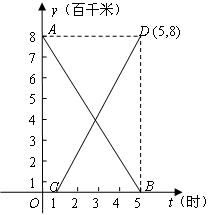

（本小题满分12分）
海安县政府大力扶持大学生开展创业．王强在县政府的扶持下销售一种进价为每件20元的护眼台灯．销售过程中发现，每月销售量y（件）与销售单价x（元）之间的关系可近似的看作一次函数：．
（1）设王强每月获得利润为w（元），当销售单价定为多少元时，每月可获得最大利润？
（2）如果王强想要每月获得2000元的利润，那么销售单价应定为多少元？
（3）根据物价部门规定，这种护眼台灯的销售单价不得高于32元，如果王强想要每月获得的利润不低于2000元，那么他每月的成本最少需要多少元？

宾馆厨房的桌子上整齐叠放着若干只形状一样的碗，它的主视图如下，请你画出它的俯视图。设叠放这种碗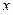只叠放高度为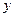厘米，经实验发现，当叠放这种碗5只时，叠放高度为12厘米；当叠放这种碗8只时，叠放高度为15.6厘米。求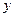（厘米）与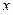（只）之间的函数关系，并指出这种碗的深度是多少？

（共8分）
如图，直线与双曲线交于A、B两点，连接OA、OB.

(1)求A、B两点的坐标；
(2)求△AOB的面积.

已知,与成正比，与成正比，当时，,当,，求y与x的函数解析式

如图，反比例函数y＝(m≠0)与一次函数y＝kx＋b(k≠0)的图象
相交于A、B两点，点A的坐标为(－6，2)，点B的坐标为(3，n)．

（1）求反比例函数和一次函数的解析式．
（2）直接写出使反比例函数值大于一次函数值的x的取值范围

(本题10分) 
已知一次函数y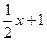＝的图象与x轴交于点A．与轴交于点；二次函数图象与一次函数y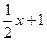＝的图象交于、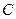两点，与轴交于、两点且的坐标为

（1）求二次函数的解析式；
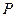（2）在轴上是否存在点P，使得△是直角三角形？若存在，求出所有的点，若不存在，请说明理由。

如图所示，某地区对某种药品的需求量y₁（万件），供应量y₂（万件）与价格x（元/件）分别近似满足下列函数关系式：y₁=－x + 70，y₂=2x－38，需求量为0时，即停止供应.当y₁=y₂时，该药品的价格称为稳定价格，需求量称为稳定需求量.

（1）求该药品的稳定价格与稳定需求量.
（2）价格在什么范围内，该药品的需求量低于供应量？
（3）由于该地区突发疫情，政府部门决定对药品供应方提供价格补贴来提高供货价格，以利提高供应量.根据调查统计，需将稳定需求量增加6万件，政府应对每件药品提供多少元补贴，才能使供应量等于需求量.

(本题满分12分)已知：如图一次函数y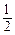＝x＋1的图象与x轴交于点A，与y轴交于点B；二次函数y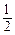＝x2＋bx＋c的图象与一次函数y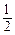＝x＋1的图象交于B、C两点，与x轴交于D、E两点且D点坐标为(1，0)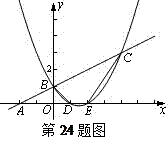

(1)求二次函数的解析式；
(2)求四边形BDEC的面积S；
(3)在x轴上是否存在点P，使得△PBC是以P为直角顶点的直角三角形？若存在，求出所有的点P，若不存在，请说明理由．

(本题满分10分)某商店经营一种小商品，进价为2.5元，据市场调查，销售单价是13.5元时平均每天销售量是500件，而销售价每降低1元，平均每天就可以多售出100件
(1)假定每件商品降价x元，商店每天销售这种小商品的利润是y元，请写出y与x间的函数关系式，并注明x的取值范围．
(2)每件小商品销售价是多少元时，商店每天销售这种小商品的利润最大？最大利润是多少？(注：销售利润＝销售收入－购进成本)

国家推行“节能减排，低碳经济”政策后，某环保节能设备生产企业的产品供不应求．若该企业的某种环保设备每月的产量保持在一定的范围，每套产品的生产成本不高于50万元，每套产品的售价不低于90万元．已知这种设备的月产量x（套）与每套的售价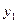（万元）之间满足关系式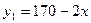，月产量x（套）与生产总成本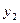（万元）存在如图所示的函数关系.

（1）直接写出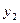与x之间的函数关系式；
（2）求月产量x的范围；
（3）当月产量x（套）为多少时，这种设备的利润W（万元）最大？最大利润是多少？

某公司有甲、乙两个绿色农产品种植基地，在收获期这两个基地当天收获的某种农产品， 一部份存入仓库，另一部分运往外地销售。根据经验，该农产品在收获过程中两个种植基地累积总产量y (吨)与收获天数x (天)满足函数关系y=2x+3 (1£x£10且x为整数)。该农产品在收获过程中甲、乙两基地的累积产量分别占两基地累积总产量的百分比和甲、乙两基地累积存入仓库的量分别占甲、乙两基地的累积产量的百分比如下表：

项目	该基地的累积产量占 两基地累积总产量的百分比	该基地累积存入仓库的量占 该基地的累积产量的百分比
百分比
种植基地
甲	60%	85%
乙	40%	22.5%

(1) 请用含y的代数式分别表示在收获过程中甲、乙两个基地累积存入仓库的量；
(2) 设在收获过程中甲、乙两基地累积存入仓库的该种农产品的总量为p(吨)，请求出p(吨)与收获天数x(天)的函数关系式；
(3) 在(2)基础上，若仓库内原有该农产品42.6吨，为满足本地市场需求，在此收获期开始 的同时，每天从仓库调出一部分该种农产品投入本地市场，若在本地市场售出的该种农产品总量m(吨)与收获天数x(天)满足函数关系m= -x2+13.2x-1.6 (1£x£10且x为整数)。
问在此收获期内连续销售几天，该农产品库存量达到最低值？最低库存量是多少吨？