河南省郑州初三模拟数学卷
某汽车制造厂开发了一款新式电动车,计划一年内投入生产安装.由于抽调不出足够的熟练工来完成新式电动车的安装,工厂决定招聘一些新工人;他们经过培训后上岗,也能独立进行电动车的安装,生产开始后,调研部门发现;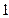 名熟练工和
名熟练工和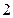 名新工人每月共可安装
名新工人每月共可安装 辆电动车;
辆电动车;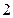 名熟练工和
名熟练工和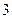 名新工人每月共可安装
名新工人每月共可安装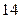 辆电动车.问每名熟练工和新工人每月分别可以安装多少辆电动车?
辆电动车.问每名熟练工和新工人每月分别可以安装多少辆电动车?
某中学数学活动小组为了调查居民的用水情况,从某社区的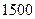 户家庭中随机抽取了
户家庭中随机抽取了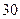 户家庭的月用水量,结果如下表所示:
户家庭的月用水量,结果如下表所示:
| 月用水量(吨) |
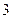 |
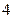 |
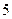 |
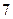 |
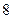 |
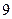 |
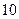 |
| 户数 |
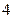 |
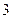 |
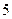 |
 |
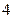 |
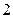 |
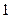 |
(1)求这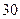 户家庭月用水量的平均数、众数和中位数;
户家庭月用水量的平均数、众数和中位数;
(2)根据上述数据,试估计该社区的月用水量;
(3)由于我国水资源缺乏,许多城市常利用分段计费的办法引导人们节约用水,即规定每个家庭的月基本用水量为 (吨),家庭月用水量不超过
(吨),家庭月用水量不超过 (吨)的部分按原价收费,超过
(吨)的部分按原价收费,超过 (吨)的部分加倍收费.你认为上述问题中的平均数、众数和中位数中哪一个量作为月基本用水量比较合理?简述理由.
(吨)的部分加倍收费.你认为上述问题中的平均数、众数和中位数中哪一个量作为月基本用水量比较合理?简述理由.
让深圳人期待了五年之久的出租车运价调整新方案终于于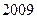 年
年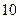 月开始执行,深圳市红色的士调价前后的收费标准对比如下:调整前,起步价
月开始执行,深圳市红色的士调价前后的收费标准对比如下:调整前,起步价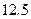 元/
元/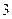 公里,
公里,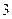 公里后里程价
公里后里程价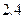 元/公里,无返空费;调整后,起步价
元/公里,无返空费;调整后,起步价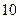 元/
元/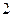 公里,
公里,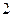 公里后里程价
公里后里程价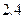 元/公里,总路程超过
元/公里,总路程超过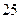 公里的,超出部分按里程价的
公里的,超出部分按里程价的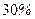 加收返空费.(不考虑红灯等因素)
加收返空费.(不考虑红灯等因素)
(1)小明去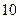 公里外的公园玩,请你估算一下,调价前后乘坐出租车的车费;
公里外的公园玩,请你估算一下,调价前后乘坐出租车的车费;
(2)网上流传“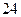 公里换车”规避返空费的方法:即乘客的行程超过
公里换车”规避返空费的方法:即乘客的行程超过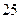 公里,就在
公里,就在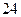 公里处下车,换乘另一辆出租车.以下为行程为
公里处下车,换乘另一辆出租车.以下为行程为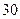 、
、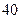 公里换与不换的方法:
公里换与不换的方法:
①若行程为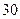 公里:不换车,总费用为:
公里:不换车,总费用为: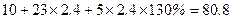 元;
元;
换车,总费用为: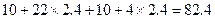 元,因此,行程
元,因此,行程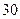 公里若换车,则费用反而增加
公里若换车,则费用反而增加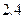 元.所以,行程为
元.所以,行程为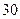 公里不换车.
公里不换车.
②若行程为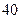 公里:不换车,总费用为:
公里:不换车,总费用为: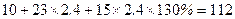 元,若换车,总费用为:
元,若换车,总费用为: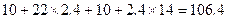 元,则可节约
元,则可节约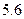 元.所以,行程为
元.所以,行程为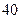 公里换车.
公里换车.
若设行程为 公里(
公里(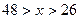 ),不换车的费用
),不换车的费用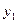 (元),换车的费用
(元),换车的费用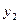 (元),
(元),
则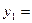 ;
; .
.
请你帮忙计算一下,行程超过多少公里后换车会就会节约费用.
我们给出如下定义:若一个四边形中存在相邻两边的平方和等于一条对角线的平方,则称这个四边形为勾股四边形,这两条相邻的边称为这个四边形的勾股边.
(1)写出你学过的特殊四边形中是勾股四边形的两种图形的名称 , ;
(2)如图16(1),已知格点(小正方形的顶点)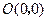 ,
,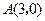 ,
,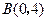 ,请你画出
,请你画出
以格点为顶点,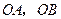 为勾股边且对角线相等的勾股四边形
为勾股边且对角线相等的勾股四边形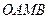 ;
;
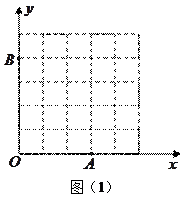 |
(3)如图16(2),将 绕顶点
绕顶点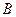 按顺时针方向旋转
按顺时针方向旋转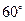 ,得到
,得到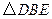 ,连结
,连结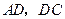 ,
,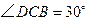 .求证:
.求证: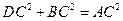 ,即四边形
,即四边形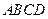 是勾股四边形
是勾股四边形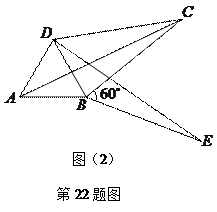
小敏在今年的校运动会跳远比赛中跳出了满意一跳,函数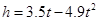 (t的单位:s,h的单位:m)可以描述他跳跃时重心高度的变化,则他起跳后到重心最高时所用的时间是( )
(t的单位:s,h的单位:m)可以描述他跳跃时重心高度的变化,则他起跳后到重心最高时所用的时间是( )
| A.0.71s | B.0.70s | C.0.63s | D.0.36s |
一个密闭不透明的盒子里有若干个白球,在不允许将球倒出来的情况下,为估计白球的个数,小刚向其中放入8个黑球,摇匀后从中随机摸出一个球记下颜色,再把它放回盒中,不断重复,共摸球400次,其中88次摸到黑球,估计盒中大约有白球( )
| A.28个 | B.30个 | C.36个 | D.42个 |
如图,一艘轮船向正东方向航行,上午9时测得它在灯塔P的南偏西30°方向,距离灯塔120海里的M处,上午11时到达这座灯塔的正南方向的N处,则这艘轮船在这段时间内航行的平均速度是 海里/时
在“百度”搜索引擎中输入“NBA”,能搜索到与之相关的网页约为45 400 000个,将这个数用科学记数法表示为
| A.4.54×106 | B.45.4×106 | C.4.54×107 | D.4.54×108 |
木匠师傅要把边长为1.6m的正六边形木板桌面改成圆形桌面,则改成的圆形桌面的最大直径为
| A.3.2 m | B.1.6 m | C.0.8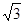 m m |
D.1.6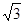 m m |
刘翔为了备战2008年奥运会,刻苦进行110米跨栏训练,为判断他的成绩发挥是否稳定,教练对他10次训练的成绩进行统计分析,则教练需了解刘翔这10次成绩的
| A.众数 | B.方差 | C.平均数 | D.频数 |
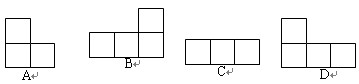
如下图是由几个相同的小正方体搭建的几何体的俯视图,小正方形中的数字表示在该位置的小正方体的个数,这个几何体的主视图是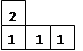
如右图所示为农村一古老的捣碎器,已知支撑柱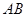 的高为0.3米,踏板
的高为0.3米,踏板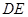 长为1.6米,支撑点
长为1.6米,支撑点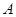 到踏脚
到踏脚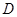 的距离为0.6米,原来捣头点
的距离为0.6米,原来捣头点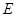 着地,现在踏脚
着地,现在踏脚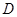 着地,则捣头点
着地,则捣头点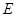 上升了
上升了 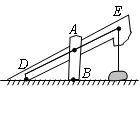
| A.1.2米 | B.1米 | C.0.8米 | D.1.5米 |
如图,已知扇形OACB中,∠AOB=60°,弧AB长为4π,⊙Q和弧AB、OA、OB分别相切于点C、D、E,求⊙Q的周长为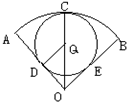
A.4π
B.8π
C.2π
D.以上都不对
在某次数学竞赛考试中,有三道“四选一”的单项选择题(每题都给出A,B,C,D四个选择项,其中只有一个正确);小明对第一题已正确地排除A、C选择项不能选,对第二题已正确地排除B、D选择项不能选,对第三题已正确地排除A选择项不能选,对其它选择项毫无把握;他便从排除后剩下的选择项中随机选择一个选项作为答案完成这三道单项选择题的解答.问:小明三题全错的概率比他答对了两道题的概率大吗?请写出你的理由。
蓝军与红军进行军事演习,如图,红军的潜艇从A海港出发,沿正东方向航行,到正东方向由红军控制的海港B处,A、B两港相距200海里,在海港A的北偏东60°方向、海港B的西北方向有一海岛C被蓝军控制,在海岛C周围90海里的区域是蓝军的侦察范围。问红军的潜艇会不会进入到蓝军的侦察区域内?海港B是否处于海岛C上的蓝军侦察范围内?请说明你的理由。
某农户以前在山上种了脐橙果树44株,前两年已有所收获。现进入第三年收获期。收获时,先随意采摘5株果树上的脐橙,称得每株果树上的脐橙质量如下(单位:千克):35,35,34,39,37
(1)根据样本平均数估计,这年脐橙的总产量约是多少?
(2)若市场上的脐橙售价为每千克5元,则这年该农户卖脐橙的收入将达多少元?
(3)已知该农户第一年卖脐橙的收入为5500元,根据以上估算,试求第二年、第三年卖脐橙收入的年平均增长率是多少?
如图,点 是等边
是等边 内一点,
内一点,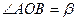 ,
, 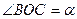 .将
.将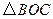 绕点
绕点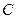 按顺时针方向旋转
按顺时针方向旋转 得
得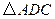 ,连接
,连接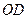 .
.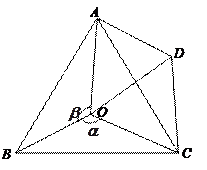
(1)当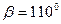 ,
,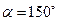 时,试判断
时,试判断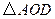 的形状,并说明理由。
的形状,并说明理由。
(2)探究:若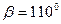 ,那么
,那么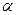 为多少度,
为多少度,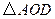 是等腰三角形?
是等腰三角形?
(只要写出探究结果)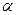 =" " 。
=" " 。
(3)请写出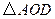 是等边三角形时
是等边三角形时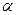 、
、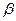 的度数。
的度数。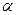 =" " 度;
=" " 度; 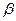 =" " 度。
=" " 度。
设边长为2a的正方形的中心A在直线l上,它的一组对边垂直于直线l,半径为r的⊙O的圆心O在直线l上运动,点A、O间距离为d.
(1)如图①,当r<a时,根据d与a、r之间关系,将⊙O与正方形的公共点个数填入下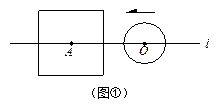
表:(6分)
| d、a、r之间关系 |
公共点的个数 |
| d>a+r |
|
| d=a+r |
|
| a-r<d<a+r |
|
| d=a-r |
|
| d<a-r |
|
所以,
当r<a时,⊙O与正方形的公共点的个数可能有 个;
(2)如图②,当r=a时,根据d与a、r之间关系,将⊙O与正方形的公共点个数填入下表:(5分)
| d、a、r之间关系 |
公共点的个数 |
| d>a+r |
|
| d=a+r |
|
| a≤d<a+r |
|
| d<a |
|
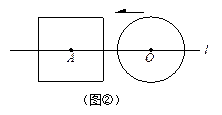
所以,当r=a时,⊙O与正方形的公共点个数可能有 个;
(3)如图③,当⊙O与正方形有5个公共点时,试说明r=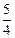 a;(5分)
a;(5分)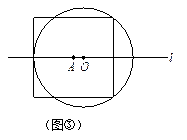
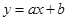 的图象经过二、三、四象限,则二次函数
的图象经过二、三、四象限,则二次函数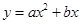 的图象只可能是( )
的图象只可能是( )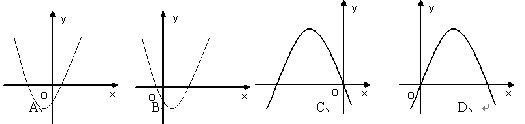
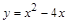 的对称轴是 ( )
的对称轴是 ( )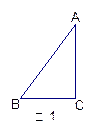

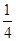
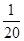
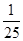

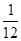 B
B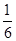 C
C D
D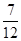
 ,使它经过原点,写出平移后抛物线的一个解析式_______
,使它经过原点,写出平移后抛物线的一个解析式_______ 的值,使二次函数
的值,使二次函数 的图象同时满足下列条件:①开口向下,②当
的图象同时满足下列条件:①开口向下,②当 时,
时, 随
随 的增大而增大;当
的增大而增大;当 时,
时,
 的顶点坐标为( , )
的顶点坐标为( , )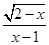 有意义,则x的取值范围为 ( )
有意义,则x的取值范围为 ( )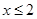
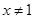
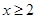
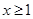
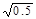 ,
,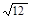 ,
,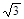 ,
,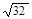 中任取两个数相乘.积为有理数的概率为
中任取两个数相乘.积为有理数的概率为 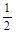
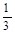
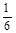
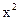 - 9
- 9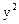 =" "
=" "
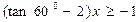 的最大整数解
的最大整数解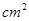
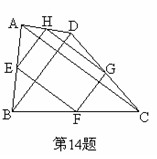
 与直线
与直线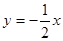 交于A、B两点,AC⊥y轴于点C,若
交于A、B两点,AC⊥y轴于点C,若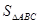 = 2,则
= 2,则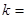
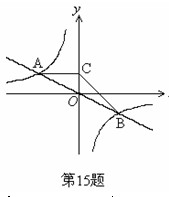
 .
.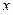 只叠放高度为
只叠放高度为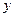 厘米,经实验发现,当叠放这种碗5只时,叠放高度为12厘米;当叠放这种碗8只时,叠放高度为15.6厘米。求
厘米,经实验发现,当叠放这种碗5只时,叠放高度为12厘米;当叠放这种碗8只时,叠放高度为15.6厘米。求
 粤公网安备 44130202000953号
粤公网安备 44130202000953号