江苏省海安县初三第一学期期末数学卷doc
如图,△ABC中,AB=4,BC=6cm,AC=8cm,∠B与∠C的角平分线交于点P,EF经过点P,且EF∥BC,点E在AB上,点F在AC上,则EF= cm.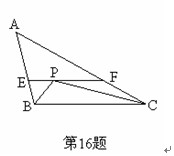
如图,小芳和小丽想测量学校旗杆的高度,她们来到操场,小芳测得小丽身高1.6米,在阳光下的影子长度为2.4米,她想立刻测量旗杆的影长时,因旗杆靠近一教学楼,影子不全落在地面上,有一部分落在墙上,测得落在地面上影长为12米,留在墙上的影高为2米,求旗杆的高度.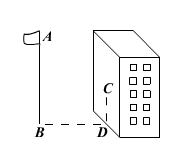
(共7分)
小江计划将鱼在年底打捞出来运往某地出售,为了预订车辆运输,必须知道鱼塘内共有多少千克的鱼,他第一次从鱼塘中打捞出100条鱼,共240kg,作上记号后,又放回鱼塘.过了两天,又捞出200条鱼,共510kg,且发现其中有记号的鱼只有4条.
(1)估计鱼塘中总共有多少条鱼?
(2)若平均每千克鱼可获利润5元,预计小江今年卖鱼总利润约多少钱?
国庆期间青年旅行社为吸引市民去东部华侨城游玩,推出如下收费标准:
某单位组织员工去东部华侨城游玩,共支付给青年旅行社旅游费用10000元.请问,该单位共组织多少名员工去东部华侨城游玩?
如图 某货船以16海里/时的速度将一批重要物资从A处运往正东方向的M处,在点A处测得某岛C在北偏东45°的方向上.该货船航行30分钟后到达B点,此时再测得该岛在北偏东30°的方向上,已知在C岛周围12海里的区域内有暗礁.若继续向正东方向航行,该货船有无触礁危险?试说明理由.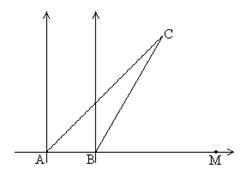
下列命题正确的是( )
| A.对角线相等的四边形是矩形 |
| B.菱形的对角线互相平分 |
| C.三角形的一条中位线将三角形分为面积相等的两部分 |
| D.顺次连接矩形各边中点得到的四边形是正方形 |
已知二次函数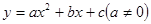 的图象如图所示,有下列5个结论:
的图象如图所示,有下列5个结论:
① >0;②b<a+c;③a+b+c>0;④2a-b>0;⑤9a-3b+c<0其中正确的有
>0;②b<a+c;③a+b+c>0;④2a-b>0;⑤9a-3b+c<0其中正确的有
| A.2个 | B.3个 | C.4个 | D.5个 |
某电器城购进一批单价为8元的节能灯管,如果按每支10元出售,那么每天可销售100支,经调查发现,这种节能灯管的售价每提高1元,其销售量相应减少5支,为了每天获得最大利润,该电器城应将这种灯管的售价定为每支多少元?每天获得的最大利润是多少?
下列事件是随机事件的是( ▲ ).
| A.在一个标准大气压下,加热到100℃,水沸腾 |
| B.购买一张福利彩票,中奖 |
| C.有一名运动员奔跑的速度是30米/秒 |
| D.在一个仅装着白球和黑球的袋中摸球,摸出红球 |
如图所示,已知点E、F分别是△ABC中AC、AB边的中点,BE、CF相交于点G,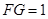 ,则CF的长为( ).
,则CF的长为( ). 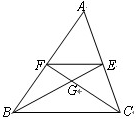
A.2
B.1.5
C.3
D.4
把抛物线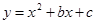 的图象向右平移3个单位,再向下平移2个单位,所得图象的解析式为
的图象向右平移3个单位,再向下平移2个单位,所得图象的解析式为 ,则
,则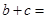 ( ▲ ).
( ▲ ).
| A.12 | B.9 | C.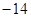 |
D.10 |
如图,△ABC是直角边长为4的等腰直角三角形,直角边AB是半圆O1的直径,半圆O2过C点且与半圆O1相切,则图中阴影部分的面积是( )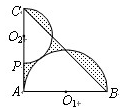
A.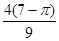 |
B.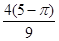 |
C.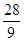 |
D. |
如图,在平行四边形ABCD中,点E在边BC上,BE:EC=1:2,连接AE交BD于点F,则△BEF的面积与△ADF的面积之比为 ▲ .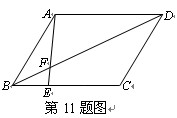
将直角边长为3cm的等腰直角△ABC绕点A逆时针旋转15°后,得到△ADE,则图中阴影部分的面积为 ▲ cm2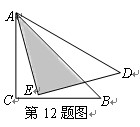
如图所示,AB为⊙O的直径,P点为其半圆上一点,∠POA=40°,C为另一半圆上任意一点(不含A、B),则∠PCB= ▲ 度.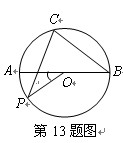
一个密码箱的密码, 每个数位上的数都是从0到9的自然数,若要使不知道密码的人一次就拨对密码的概率小于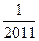 ,则密码的位数至少需要 ▲ 位
,则密码的位数至少需要 ▲ 位
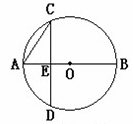
如图,DB为半圆的直径,A为BD延长线上一点,AC切半圆于点E,BC⊥AC于点C, 交半圆于点F.已知BD=2,设AD=x,CF=y,则y关于x的函数解析式是 ▲ .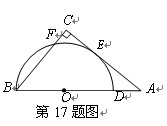
如图,在Rt△ABC中,∠A=90°,AB=AC=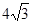 ,点D为AC的中点,点E在边BC 上,且ED⊥BD,则△CDE的面积是 ▲ .
,点D为AC的中点,点E在边BC 上,且ED⊥BD,则△CDE的面积是 ▲ .
(本小题8分)
关于x的一元二次方程 有两个不相等的实数根.
有两个不相等的实数根.
(1)求k的取值范围.
(2)请选择一个k的负整数值,并求出方程的根
(本小题10分)
抛物线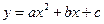 经过点O(0,0),A(4,0),B(2,2).
经过点O(0,0),A(4,0),B(2,2).
(1)求该抛物线的解析式;
(2)画出此抛物线的草图;
(3)求证:△AOB是等腰直角三角形;
(4)将△AOB绕点O按顺时针方向旋转135°得△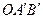 ,写出边
,写出边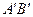 的中点P的 坐标,试判定点P是否在此抛物线上,并说明理由.
的中点P的 坐标,试判定点P是否在此抛物线上,并说明理由.
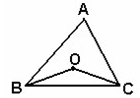
(本小题8分)如图,在△ABC中,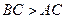 ,点D在BC上,且DC=AC,
,点D在BC上,且DC=AC,
∠ACB的平分线CF交AD于点F,点E是AB的中点,连结EF.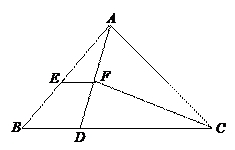
求证:EF∥BC;
若△ABD的面积为6,求四边形BDFE的面积.
(本小题满分10分)
如图,直线AB经过⊙O上的点C,并且OA=OB,CA=CB,⊙O交直线OB于E、D,连接EC、CD.
(1)求证:直线AB是⊙O的切线;
(2)试猜想BC,BD,BE三者之间的等量关系,并加以证明
(本小题满分8分)
“中秋”节前,妈妈去超市购买了大小、质量都相同的火腿月饼和豆沙月饼若干,放入不透明的盒中,此时随机取出火腿月饼的概率为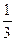 ; 小明发现爷爷喜欢吃的火腿月饼偏少,又叫爸爸去买了同样的5只火腿月饼和1只豆 沙月饼放入同一盒中,这时随机取出火腿月饼的概率为
; 小明发现爷爷喜欢吃的火腿月饼偏少,又叫爸爸去买了同样的5只火腿月饼和1只豆 沙月饼放入同一盒中,这时随机取出火腿月饼的概率为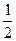 .
.
(1)请计算出妈妈买的火腿月饼和豆沙月饼各有多少只?
(2)若妈妈从盒中取出火腿月饼4只、豆沙月饼6只送给奶奶后,再让小明从盒中任取2只(取出不放回),问恰有火腿月饼、豆沙月饼各1只的概率是多少?
(可用列表法进行解答)
如图,⊙O是△ABC的外接圆,FH是⊙O 的切线,切点为F,FH∥BC,连结AF交BC于E,∠ABC的平分线BD交AF于D,连结BF.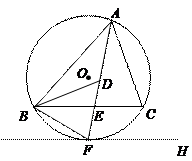
(1)求证:AF平分∠BAC;
(2)求证:BF=FD;
(3)若EF=3,DE=2,求AD的长.
(本小题满分12分)
海安县政府大力扶持大学生开展创业.王强在县政府的扶持下销售一种进价为每件20元的护眼台灯.销售过程中发现,每月销售量y(件)与销售单价x(元)之间的关系可近似的看作一次函数: .
.
(1)设王强每月获得利润为w(元),当销售单价定为多少元时,每月可获得最大利润?
(2)如果王强想要每月获得2000元的利润,那么销售单价应定为多少元?
(3)根据物价部门规定,这种护眼台灯的销售单价不得高于32元,如果王强想要每月获得的利润不低于2000元,那么他每月的成本最少需要多少元?
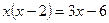
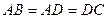 =4,
=4,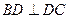 ,E为BC中点,连结DE.
,E为BC中点,连结DE. 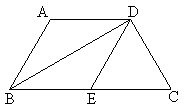
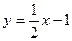 与双曲线
与双曲线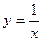 交于A、B两点,连接OA、OB.
交于A、B两点,连接OA、OB.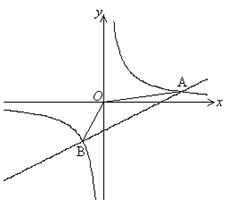
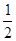
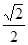
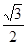
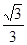
 图象上的点为( )
图象上的点为( )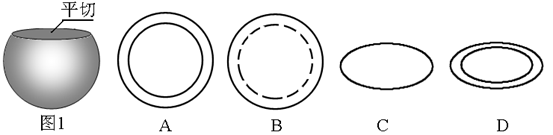
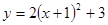 的顶点坐标是( )
的顶点坐标是( ) cm
cm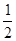

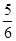
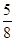
 cm
cm cm
cm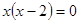 的解为
的解为 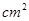
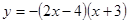 的图象与x轴的交点坐标为
的图象与x轴的交点坐标为  与⊙
与⊙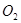 相切,⊙
相切,⊙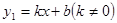 与反比例函数
与反比例函数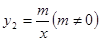 的图象交于A、B两点,则使
的图象交于A、B两点,则使 <
<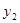 的x的取值范围是
的x的取值范围是 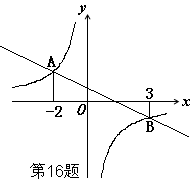

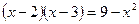
 中,∠A=45°,
中,∠A=45°,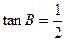 ,
,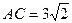 cm,求AB的长度
cm,求AB的长度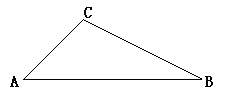
 有意义,a的取值范围是( ▲ ).
有意义,a的取值范围是( ▲ ).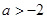
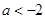
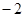

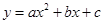 的图像如图所示,当函数值
的图像如图所示,当函数值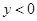 时,x的取值范围为
时,x的取值范围为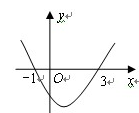
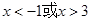

 x≥3
x≥3 ≤x≤3
≤x≤3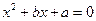 有一个根是
有一个根是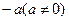 ,则下列代数式的值恒为常数的是( ▲ ).
,则下列代数式的值恒为常数的是( ▲ ).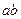
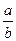
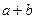
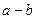
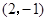 关于原点对称的点B的坐标为 ▲
关于原点对称的点B的坐标为 ▲ 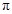 ).
).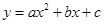 的图象如图,则下列5个代数式:①ac,②
的图象如图,则下列5个代数式:①ac,②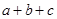 ,③
,③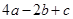 ,④
,④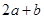 ,⑤
,⑤ ,⑥
,⑥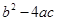 中,其值大于0的序号为 ▲
中,其值大于0的序号为 ▲ 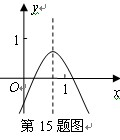
 的两个实数根,那么
的两个实数根,那么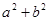 的最小值是 ▲ .
的最小值是 ▲ .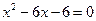
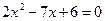 (用配方法解)
(用配方法解)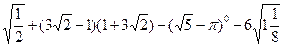
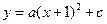 与y轴交于点C(0,
与y轴交于点C(0,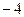 ), 与x轴交于点A、 B,点A的坐标为(2,0).
), 与x轴交于点A、 B,点A的坐标为(2,0).
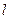 与该抛物线交于点Q,与直线BC交于点F,点M 的坐标为(
与该抛物线交于点Q,与直线BC交于点F,点M 的坐标为(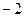 ,0).问:是否存在这样的直线
,0).问:是否存在这样的直线 粤公网安备 44130202000953号
粤公网安备 44130202000953号