初中数学一次函数的最值解答题

小聪和小明沿同一条路同时从学校出发到图书馆查阅资料，学校与图书馆的路程是4千米，小聪骑自行车，小明步行，当小聪从原路回到学校时，小明刚好到达图书馆，图中折线O－A－B－C和线段OD分别表示两人离学校的路程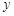（千米）与所经过的时间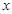（分钟）之间的函数关系，请根据图象回答下列问题：
（1）小聪在图书馆查阅资料的时间为      分钟，小聪返回学校的速度为     千米/分钟．
（2）请你求出小明离开学校的路程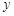(千米)与所经过的时间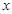(分钟)之间的函数关系；
（3）当小聪与小明迎面相遇时，他们离学校的路程是多少千米？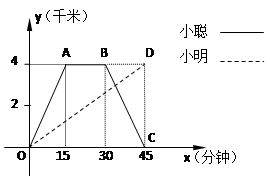

如图，矩形OABC的边OA在x轴正半轴上，边OC在y轴正半轴上，B点的坐标为(1，3)．矩形O'A'BC'是矩形OABC绕B点逆时针旋转得到的．O'点恰好在x轴的正半轴上， O'C'交AB于点D.

(1)求点O'的坐标，并判断△O'DB的形状（要说明理由）(4分)
(2)求边C'O'所在直线的解析式．(4分)
(3)延长BA到M使AM=1，在(2)中求得的直线上是否存在点P，使得ΔPOM是以线段OM为直角边的直角三角形?若存在，请直接写出P点的坐标；若不存在，请说明理由．(2分)

甲、乙两组工人同时加工某种零件，乙组工作中有一次停产更换设备，更换设备后，乙组的工作效率是原来的2倍．两组各自加工零件的数量(件)与时间(时)的函数图象如图所示．

(1)求甲组加工零件的数量y与时间之间的函数关系式．(2分)
(2)当x=2.8时，甲、乙两组共加工零件         件；
乙组加工零件总量的值为         ．(4分)
(3) 加工的零件数达到230件装一箱，零件装箱的时间忽略不计，若甲、乙两组加工出的零件合在一起装箱，当甲组工作多长时间恰好装满第2箱？ (2分)

某长途汽车站规定，乘客可以免费最多携带质量a千克的行李，若超过a千克则需购买行李票，且行李票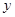(元)与行李质量(千克)间的一次函数关系式为，现知贝贝带了60千克的行李，交了行李费7元。
(1)若京京带了80千克的行李，则该交行李费多少元？
(2)求a的值．

某工厂有两批数量相同的产品生产任务,分别交给甲、乙两个小组同时进行生产．如图是反映生产数量y(件)与生产时间x(h)之间关系的部分图象．请解答下列问题：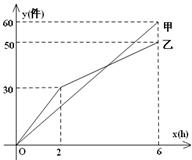

⑴乙小组生产到30 件时，用了      h．生产6 h时，甲小组比乙小组多生产了      件；
⑵ 请你求出：
①甲小组在0≤x≤6的时段内，y与x之间的函数关系式；(直接写出结论)
②乙小组在2≤x≤6的时段内，y与x之间的函数关系式；(直接写出结论)
③生产几小时后，甲小组所生产的数量开始超过乙小组？  (要求写出过程)
⑶ 如果甲小组生产速度不变，乙小组在生产6 h后，生产速度增加到12 件/h，结果两小组同时完成了任务．问甲小组从开始生产到完工所生产的数量为多少件？(要求写出过程)

如图，在平面直角坐标系xoy中，已知直线l₁:y=x与直线l₂：y=－x+6相交于点M，直线l₂与x轴相较于点N.
求M，N的坐标；
在矩形ABCD中，已知AB=1，BC=2，边AB在x轴上，矩形ABCD沿x轴自左向右以每秒1个
单位长度的速度移动.设矩形ABCD与△OMN的重叠部分的面积为S.移动的时间为t（从点B与点O重合时开始计时，到点A与点N重合时计时结束）。直接写出S与自变量t之间的函数关系式（不需要给出解答过程）；
在（2）的条件下，当t为何值时，S的值最大？并求出最大值.

 

某工厂生产A、B两种产品共50件，其生产成本与利润如下表：

	A种产品	B种产品
成本 （万元／件）	0.6	0.9
利润 （万元／件）	0.2	0.4

 
若该工厂计划投入资金不超过40万元，且希望获利超过16万元，问工厂有哪几种生产方案？哪种生产方案获利润最大？最大利润是多少？

今年春季，我省云南、贵州等西南地区遇到多年不遇旱灾，“一方有难，八方支援”，为及时灌溉农田，丰收农机公司决定支援上坪村甲、乙、丙三种不同功率柴油发电机共10台（每种至少一台）及配套相同型号抽水机4台、3台、2台，每台抽水机每小时可抽水灌溉农田1亩。现要求所有柴油发电机及配套抽水机同时工作一小时，灌溉农田32亩。
（1）设甲种柴油发电机的数量为x台，乙种柴油发电机数量y台。
①用含ｘ、ｙ的式子表示丙种柴油发电机的数量；
②求出ｙ与ｘ的函数解析式；
（２）已知甲、乙、丙柴油发电机每小时费用分别为１３０元、１２０元 、１００元，应如何安排三种柴油发电机的数量，既能按要求抽水灌溉，同时柴油发电机总费用ｗ最少？ 

大学生李萌同学利用暑假参加社会实践，为某报社推销报纸，订购价格是每份0.7元，销售价是每份1元，卖不掉的报纸由报社发行部以每份0.2元回收，在一个月内（以31天计算）约有20天每天可卖出100份，其余11天每天可卖出60份，但报社发行部要求每天订购的报纸份数必须相同，若每天订购x份为自变量，该月所获得的利润y（元）为x的函数.
（1）写出y与x的函数关系式，并指出x自变量的取值范围。
（2）李萌同学应该每天订购多少份该报纸，才能使该月获得的利润最大？并求出这个最大值。

如图，在边长为2的正方形ABCD的一边BC上，一点P从B点运动到C点，设BP=x，四边形APCD的面积为y.
⑴ 写出y与x之间的函数关系式及x的取值范围；
⑵ 说明是否存在点P，使四边形APCD的面积为1.5？  

已知某一次函数自变量x的取值范围是0≤x≤10，函数y的取值范围，10≤y≤30 , 求此函数解析式.

如图，已知直线，直线，直线、分别交x轴于B、C两点，、相交于点A。
(1) 求A、B、C三点坐标；
(2) 求△ABC的面积。

在平面直角坐标系内，已知点A(0，6)、点B(8，0)，动点P从点A开始在线段AO上以每秒1个单位长度的速度向点O移动，同时动点Q从点B开始在线段BA上以每秒2个单位长度的速度向点A移动，设点P、Q移动的时间为t秒．

(1)求直线AB的解析式；
(2)当t为何值时，以点A、P、Q为顶点的三角形与△AOB相似?
(3)当t=2秒时，求四边形OPQB的面积．

为响应市政府“创建国家森林城市”的号召，某小区计划购进A、B两种树苗共17棵，已知A种树苗每棵80元，B种树苗每棵60元．
（1）若购进A、B两种树苗刚好用去1220元，问购进A、B两种树苗各多少棵？
（2）若购买B种树苗的数量少于A种树苗的数量，请你给出一种费用最省的方案，并求出该方案所需费用．

张勤同学的父母在外打工，家中只有年迈多病的奶奶．星期天早上，李老师从家中出发步行前往张勤家家访．6分钟后，张勤从家出发骑车到相距1200米的药店给奶奶买药，停留14分钟后以相同的速度按原路返回，结果与李老师同时到家．张勤家、李老师家、药店都在东西方向笔直大路上，且药店在张勤家与李老师家之间．在此过程中设李老师出发t（0≤t≤32）分钟后师生二人离张勤家的距离分别为S₁、S₂．S与t之间的函数关系如图所示，请你解答下列问题：
（1）李老师步行的速度为　   　；
（2）求S₂与t之间的函数关系式，并在如图所示的直角坐标系中画出其函数图象；
（3）张勤出发多长时间后在途中与李老师相遇？