初中数学一次函数的最值解答题

甲、乙两家体育用品商店出售同样的乒乓球拍和乒乓球，乒乓球拍每付定价20元，乒乓球每盒定价5元。现两家商店搞促销活动。甲店：每买一付球拍赠一盒乒乓球；乙店：按定价的9折优惠。某班级需购球拍4付，乒乓球若干盒（不少于4盒）。
（1）设购买乒乓球盒数为x（盒），在甲店购买的付款数为y_甲（元），在乙店购买的付款数为y_乙（元），分别写出在两家商店购买的付款数与乒乓球盒数x之间的函数关系式。
（2）就乒乓球盒数讨论去哪家商店买合算？

如图，直线OC、BC的函数关系式分别是y₁=x和y₂=-2x+6，动点P（x，0）在OB上运动（0<x<3），过点P作直线m与x轴垂直．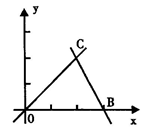

（1）求点C的坐标，并回答当x取何值时y₁>y₂？
（2）设△COB中位于直线m左侧部分的面积为s，求出s与x之间函数关系式．
（3）当x为何值时，直线m平分△COB的面积？

蜡烛燃烧，每小时耗去4.8厘米，已知蜡烛原来的长度为24厘米，设燃烧x小时后剩下的长度为y厘米．（1）写出y与x之间的函数关系式；（2）经过多长时间后，蜡烛点完？

小明平时喜欢玩“QQ农场”游戏，本学期八年级数学备课组组织了几次数学反馈性测试，小明的数学成绩如下表：

月份x（月）	9	10	11	12	…
成绩y	90	80	70	60	…

（1）以月份为x轴，成绩为y轴，根据上表提供的数据在下列直角坐标系中描点；

（2）观察①中所描点的位置关系，照这样的发展趋势，猜想y与x之间的函数关系，并求出所猜想的函数表达式；
（3）若小明继续沉溺于“QQ农场”游戏，照这样的发展趋势，请你估计元月份的期末考试中小明的数学成绩，并用一句话对小明提出一些建议．

已知一次函数y＝kx＋b的图像经过点（－1，－5），且与正比例函数的图像相交于点（2，m）.
求:（1）m的值；    
（2）一次函数y＝kx＋b的解析式；
（3）这两个函数图像与x轴所围成的三角形面积.

20个集装箱装满了甲、乙、丙三种商品共120吨，每个集装箱都只装载一种商品，根据下表提供的信息，解答以下各题：

商品类型	甲	乙	丙
每个集装箱装载量（吨）	8	6	5
每吨价值（万元）	12	15	20

 
（1）如果甲种商品装个集装箱，乙种商品装个集装箱，求 与 之间的关系式；
（2）如果其中5个集装箱装了甲种商品，求每个集装箱装载商品总价值的中位数．

如图，直线：与直线：相交于点，直线与轴交于点，平行于轴的直线分别交直线、直线于、两点（点在的左侧）
⑴点的坐标为                  ；
⑵如图1，若点在线段上，在轴上是否存在一点，使得为等腰直角三角形，若存在，求出点的坐标；若不存在，说明理由；
⑶如图2.若以点为直角顶点，向下作等腰直角，设与重叠部分的面积为，求与的函数关系式；并注明的取值范围.

已知、两地相距120千米，甲乘坐一橡皮筏从地顺流去地，2小时后，乙坐船从地出发去地.如图为甲、乙两人离地的路程（千米）与乙行进的时间（小时）的函数图象.乙到达地后，立即坐船返回.
⑴求船在静水中的速度和水流的速度；
⑵求甲、乙两人相遇的时间和距地的距离.

村有肥料200吨，村有肥料300吨，现要将这些肥料全部运往、两仓库.从村往、两仓库运肥料的费用分别为每吨20元和25元；从村往、两仓库运肥料的费用分别为每吨15元和18元；现仓库需要肥料240吨，现仓库需要肥料260吨.
⑴设村运往仓库吨肥料，村运肥料需要的费用为元；村运肥料需要的费用为元.
①写出、与的函数关系式，并求出的取值范围；
②试讨论、两村中，哪个村的运费较少？
⑵考虑到村的经济承受能力，村的运输费用不得超过4830元，设两村的总运费为元，怎样调运可使总运费最少？

已知两条直线和．
⑴在同一坐标系内作出它们的图象；
⑵求出它们的交点坐标；
⑶求出这两条直线与轴围成的三角形的面积；

在平面直角坐标系中的位置如图

⑴通过列表、描点画出直线的图象；
⑵作关于直线对称的图形，并写出各顶点的坐标；
⑶若点（，）是内部一点，则其变换后的对称点的坐标为               .

如图，已知直线AB与x轴交于A(6，0)点，与y轴交于B(0，10)点，点M的坐标为(0，4)，
点P(x，y)是折线O→A→B的动点(不与O点、B点重合)，连接OP、MP，设△OPM的面积为S．
(1) 求S关于x的函数表达式，并写x的取值范围；
(2) 当△OPM是以OM为底边的等腰三角形时，求S的值；
(3) 当线段MP分△OAB的面积比为1∶4时，求P点坐标．

2008年6月1日起，我国实施“限塑令”，开始有偿使用环保购物袋．为了满足市场需求，某厂家生产两种款式的布质环保购物袋，每天共生产4500个，两种购物袋的成本和售价如下表，设每天生产种购物袋个，每天共获利元．
（1）求出与的函数关系式；
（2）如果该厂每天最多投入成本10000元，那么每天最多获利多少?

有甲、乙两个蓄水池，现将甲池中的水匀速注入乙池。甲、乙两个蓄水池中水的深度（米）与注水时间（小时）之间的关系如图所示，根据图像提供的信息，回答下列问题：

（1）注水前甲池中水的深度是_____________米。（直接写出答案）。
（2）求甲池中水的深度（米）与注水时间（小时）之间的函数关系式；
（3）求注水多长时间时，甲、乙两个蓄水池中水的深度相同。

已知直线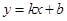经过点、.
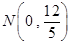（1）求直线的解析式；
（2）当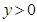时，求的取值范围；
（3）我们将横坐标、纵坐标均为整数的点称为整数点．直接写出此直线与两坐标轴围成的三角形的内部（不包含边界）的整数点的坐标．