有甲、乙两个蓄水池,现将甲池中的水匀速注入乙池。甲、乙两个蓄水池中水的深度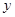 (米)与注水时间
(米)与注水时间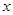 (小时)之间的关系如图所示,根据图像提供的信息,回答下列问题:
(小时)之间的关系如图所示,根据图像提供的信息,回答下列问题:
(1)注水前甲池中水的深度是_____________米。(直接写出答案)。
(2)求甲池中水的深度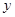 (米)与注水时间
(米)与注水时间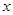 (小时)之间的函数关系式;
(小时)之间的函数关系式;
(3)求注水多长时间时,甲、乙两个蓄水池中水的深度相同。
相关知识点
推荐套卷
有甲、乙两个蓄水池,现将甲池中的水匀速注入乙池。甲、乙两个蓄水池中水的深度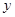 (米)与注水时间
(米)与注水时间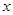 (小时)之间的关系如图所示,根据图像提供的信息,回答下列问题:
(小时)之间的关系如图所示,根据图像提供的信息,回答下列问题:
(1)注水前甲池中水的深度是_____________米。(直接写出答案)。
(2)求甲池中水的深度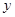 (米)与注水时间
(米)与注水时间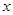 (小时)之间的函数关系式;
(小时)之间的函数关系式;
(3)求注水多长时间时,甲、乙两个蓄水池中水的深度相同。