如图，在平面直角坐标系中，△ABC的三个顶点都在格点上，点A的坐标为（2，4），请解答下列问题：
（1）画出△ABC关于x轴对称的△A1B1C1，并写出点C1的坐标（ ， ）；
（2）将△ABC的三个顶点的横、纵坐标都乘以－1，分别得到对应点A2、B2、C2，画出△A2B2C2，则△ABC和△A2B2C2关于 对称；
（3）将△ABC在网格中平移，使点B的对应点B3坐标为（－6，1），画出△A3B3C3.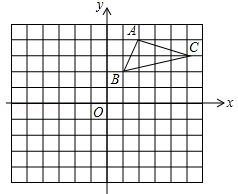
，求
的值.
)÷(
)其中
.
)÷
相关知识点
推荐套卷
如图，在平面直角坐标系中，△ABC的三个顶点都在格点上，点A的坐标为（2，4），请解答下列问题：
（1）画出△ABC关于x轴对称的△A1B1C1，并写出点C1的坐标（ ， ）；
（2）将△ABC的三个顶点的横、纵坐标都乘以－1，分别得到对应点A2、B2、C2，画出△A2B2C2，则△ABC和△A2B2C2关于 对称；
（3）将△ABC在网格中平移，使点B的对应点B3坐标为（－6，1），画出△A3B3C3.
粤公网安备 44130202000953号